Eccentricity, Conic Constant, Schwartzchild Constant and other such Definitions.

This page hopes to define the various numbers that are seen often seen in the formulas and prescriptions for surface shapes. I'm doing this because it has been a confusing thing for me to understand as the three different values don't say exactly the same things for a particular surface shape when it comes to shapes other than a sphere or a parabola. I'm going to try to make sense of all of it in this page.

You may wish to survey this page also for some additional info on the Constants.

And then there is this page which is in mixed German and English.

In Smith's "Modern Optical Engineering", p. 392, he says a conic section through the origin satisfies the equation

y² - 2 R x + (K + 1) x² = 0 where

y axis is along the optical axis
x is perpendicular to the optical axis
R is the radius of curvature
K is the conic constant

The conic (Conic Constant or Schwartzchild Constant or Aspheric Deformation Constant) -b relationship is:

Oblate ellipse K > 0
circle K=0
prolate ellipse -1< K < 0
parabola K=-1
hyperbola K < -1

And now with e = eccentricity case where:

oblate ellipse is undefined
circle e=0
prolate ellipse = 0 < e < 1
parabola e = 1
hyperbola = e>1

and finally, just for completeness as far as I know, the SHAPE parameter or Aparabolic Deformation Constant where:

oblate ellipse SH = > 1
circle SH = 1
prolate ellipse 0 < SH < 1
parabola SH = 0
hyperbola = SH < 0

and the conversion formula between the Conic Constant/Schwartzchild Constant and the Eccentricity is:
K = -e² which doesn't work for the K > 0 or the oblate ellipse case. The problem is, in that case, the optical axis is along the minor axis of the ellipse. Essentially, the eccentricity is describing the shape of the ellipse rather than its optical properties.

The Aparabolic Deformation Constant is used in the BEAM 3 ray tracing program which is the only place that I've seen it used. Why, I don't know as a little bit of programming and it could have been using the (I assume as I don't have that product at hand and somebody with the program can correct me if I'm wrong and it is the eccentricity instead) Conic Constant instead.

eccentricity is defined as you take half of the distance between the foci, which equals the center-to-focus separation. So if the distance between the two foci is 6mm and the distance from one focus to the sharp end near it is 6mm then the eccentricity e is 0.5 and thus by the above formula, the Conic Constant K is -0.25. The relation between the center separation (c) on one, and horizontal (a) and vertical semiaxis (b) is given by the formula:

c² = a² - b² To get e you then run the formula: e² = c² / a² This is why oblate ellipse has negative c² as the vertical axis is longer than horizontal axis. If the Conic Constant is the negative of the square of the eccentricity, now how can the Conic Constant of an oblate spheroid be positive? Mathematically, eccentricity is the ratio of the distances between a point called the focus and a line called the directrix, which is why a parabola has an eccentricity of 1, being the locus of all points whose distances from a fixed point and a fixed line are equal, and a circle has an eccentricity of 0, since its directrix is at infinity. Another way to derive the e value is to divide one axial distance by the other. For a prolate ellipsoid, that would be the smaller distance over the larger distance, for example, the longer distance of the shape is 4 inches wide by 2 inches high, then
e = A / B = 2 / 4 = .5

Strictly speaking, an oblate spheroid's eccentricity is the same as the prolate spheroid's with the same geometry but of an opposite sign (equal major and minor radii.).

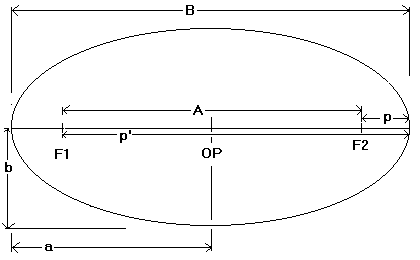
There are several ways to actually derive the e of an elipse. This drawing shows the various measurements of an elipse:

The formulas that can be used are (note the case of the letters used):

e² = (a² - b²) / a²
e = A / B
e = (p' - p) / (p' + p)

The third formula is a reformation of the second formula, deriving the values of A and B as the distance from p to the near dege of the surface is the near focus of the elipse while the p' is the distance from the far focus to the elipse. In other words, doing a concave secondary mirror for a Gregorian p is the ROC of the mirror while the p' is where the focal plane of the telescope is. A lille bit of working of these formulas will bring out all of the dimensions of the elipse.

When you look at the formulas, you'll also note that the parabola is indeed a value of 1 for e as the following indicates:

e = A / B = infinity / infinity = 1 I hope this makes sense to everybody.