On the Construction of Telescopes with Silvered Glass
Part 4
Definition of optical power
Determining its numerical value
The method we have just described, and which has been carried out a great number of times, always results in bringing optical surfaces fairly quickly to a degree of perfection which can not be surpassed. When one arrives at that point, one needs to ask whether the impossibility of making any more progress lies in the imperfection of our procedure, or whether it lies in the fact that one has reached the goal of creating a perfect surface. For us the question is not in doubt, and we will not hesitate to consider as perfect a surface which acts as far as we can tell upon light as would a mirror that corresponds precisely to the figure required by optical theory.
When a surface approaches this degree of relative perfection, one can watch an ensemble of characteristics intervene which, once understood, can serve as a guide for the worker and give notice that the work can be considered finished. At the same time as the defects disappear that are revealed by the various optical testing methods, the image, as seen under a microscope, produced by such a surface takes on a particular appearance that pleases the eye and does not disappear even when uses great enlarging powers. This remarkable appearance comes from the fact that the image is being formed by a grouping of correctly circular elements. Each of these elementary disks is in fact surrounded by a certain number of rings; but since the latter have rapidly decreasing intensities, the central disk has so much more brightness that it has the preponderance of the precise outline of the contours of light. Of the various rings that surround this disk, one can normally only see the first one. And since a dark interval separates them, the result is that this first bright ring does not bring any appreciable confusion to the image. Also, since it is superimposed on itself, it merely draws a pale belt that runs around, and is parallel to, the brightest contours of the image.
The theory of diffraction explains this phenomenon, which implies that all the rays of the convergent light come to its vertex almost completely in phase vibrationally. If we could substitute a surface that is rigorously exact for the approximate surface obtained via our experimental methods, the rays would arrive at the vertex in perfect accord. But the point of light - or rather, the narrow disk - formed by their coming together would still be surrounded by no less rings than before. Therefore there is no practical point in trying to push surfaces beyond the degree needed for the appearance of diffraction phenomena.
When these phenomena become apparent at the focus, or in other words, when the image of a point formed by the entire uncovered mirror appears in the form of a disk surrounded by rings whose brightness decreases rapidly, then we can be assured that such a mirror, aimed at any sort of object, whether on earth or in the heavens, will produce good images, and will give optical results corresponding to its diameter.
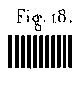 To judge the result with certainty, and to express those results in a form less vague than one normally uses in ordinary language, we should mount the mirror in a Newtonian telescope and aim it at a distant target. We should arrange this target is as to provide details placed at the limit of visibility. We construct these test targets by inscribing on a sheet of ivory a series of divisions arranged into successive groups, where the millimeter is divided into smaller and smaller parts. The thickness of the lines engraved should vary from one group to the next in such a way that the darkened portion has the same area as the interval that separates them (figure 18). If one views such a target placed at a distance, or if one observes it with too weak an optical instrument, then the different groups appear merely to have a uniform light gray color. But if one decreases the distance or uses more powerful optics, one sees that the groups that are the farthest apart resolve themselves into distinct lines, while the rest remain blurred.
To judge the result with certainty, and to express those results in a form less vague than one normally uses in ordinary language, we should mount the mirror in a Newtonian telescope and aim it at a distant target. We should arrange this target is as to provide details placed at the limit of visibility. We construct these test targets by inscribing on a sheet of ivory a series of divisions arranged into successive groups, where the millimeter is divided into smaller and smaller parts. The thickness of the lines engraved should vary from one group to the next in such a way that the darkened portion has the same area as the interval that separates them (figure 18). If one views such a target placed at a distance, or if one observes it with too weak an optical instrument, then the different groups appear merely to have a uniform light gray color. But if one decreases the distance or uses more powerful optics, one sees that the groups that are the farthest apart resolve themselves into distinct lines, while the rest remain blurred.
When we increase the enlargement and illuminate the target sufficiently, we can conclude that in the groups that uniformly gray, the blurriness of the lines cannot be attributed to the weakness of the eye. It must be entirely because the instrument resolves one of the groups and does not resolve the next one. In verifying in this way which of the groups is so close together as to be located at the limit of visibility, we obtain positive proof that the instrument can separate the parts that are separated by a certain angle, and cannot separate those that are closer together than that. It then follows that the ability of the instrument to penetrate the details of observed objects, or what we could call its optical power, is inversely proportional to the angular limit of separability of the adjacent divisions. The definitive expression of this optical power is the quotient of the distance to the target, divided by the mean interval between the finest visible divisions.
To this sort of test we have submitted a great number of mirrors of all sizes and of all focal lengths. These experiments have led us to a general expression of optical powers which is remarkably simple. We have found that this optical power is independent of focal length, that it varies only with the diameter of the mirror, and that it works out to about 150,000 units per centimeter of diameter. Without having done as many experiments on achromatic objectives, we have nonetheless discovered that, when we reduce them to their active surface diameter, they obey the same law, and that if the diameters are equal, then both lens and mirror are capable of having the same optical power.
This fact, which appears to be henceforth well-established, naturally leads one to search in the physical make up of light, and not in the imperfections of our instruments, for the obstacle which limits the extension of the effects already obtained. No matter how the optics are constructed, these instruments, as long as they approach perfection, tend to display optical powers that are in a constant ratio with the respective diameters of the ray bundles that are transmitted. One can not refrain from considering this ratio as a physical constant whose value expresses the aptitude of light for forming detailed images. In taking a millimeter as our unit of length, to which we normally relates the wavelength of light, we find, according to our experiments on optical powers, that the value of this constant is the number 1500.
This optical constant of light is intimately linked to the wavelength of light and is inversely proportional to it, so that it varies for light of different colors. This means that rays that are more easily refracted [i.e., shorter wave length light, such as blue light - trans.] produce the greatest power of definition. Experiments have confirmed this numerous times, especially via the clarity of microphotographs taken with ultraviolet light.
In general, physical constants have a reason for their existence which flows directly from the nature of the agent whose physical properties are being defined. Evidently this number 1500, which expresses in some way the separability of points of light, proceeds from the number of light waves contained in a unit of length, and multiplied by a coefficient that depends both on the procedure used to determine optical power and also on the
physiological aptitude of the retina to perceive different impressions.
It may be feared that while trying to give rise to the notion of optical power, will unwillingly provoke optical workers to announce impossible powers. But anything is liable to be distorted. To help put other observers on guard against illusory observations, we have taken care to explain precisely the way to obtain comparable measurements. We also maintain that there is an absolute limit to how high the magnification can be raised in practice by any optical instrument.
Nonetheless, we need to reserve the case where our instruments will be tested on the sky.
When the weather is very fine, it can happen that the observation of double stars with equal magnitude reveals an optical power that is higher, even up to twice the result that one would conclude from terrestrial targets. Here is an explanation for this possible anomaly. With our terrestrial target, the details we are trying to distinguish are equal spaces, alternately black and white. That was a necessary arrangement so that we could
always fall back on identical conditions of lighting and observation. But this equality of black and white is far from being the best arrangement as far as one's ability to resolve detail is concerned. In the image of such an arrangement, the width of the white areas equals their geometric area increased by the apparent diameter inherent in the width of the elementary [Airy? -- trans.] disks, so that at the moment that these white areas begin to merge, they have a width that is twice the one they would present if the white parts were infinitely small in comparison to the black parts. However, in the sky the real dimensions of double stars are infinitely small in relation tot he space between them. Thus, the width of the image of these stars is reduced to these elementary disks, which makes it so that their angular separation, with a homogeneous atmosphere, is easier than with the ivory target. We are not yet able to state how much higher the optical power determined via double stars is than that obtained by viewing the ivory target, but we are sure that the difference is considerable. A 33-cm telescope, which gave us our first opportunity to witness the fact that the blue companion star of Gamma Andromedae is a double, only had a computed optical power of 400,000, which indicated that it should theoretically only have been able to resolve one half arc-second. However, it is estimated that the angle of separation between the blue binary stars of Gamma Andromedae is 4/10 of an arc-second.
We have stated, in a general way, that in a perfect instrument the optical power is independent of the focal length. If we want to understand this fully, then we should analyze the constitution of the images of objects by following the theoretical deductions step by step. In a perfect image, the number of distinct points clearly depends on the size of the elementary disks that represent the different points of the object. Since these disks are surrounded by a dark circle which is the geometric locus of all of the points where one-half of the bundle of light rays is out of phase with the other half, it follows that the size of these disks depends both on the wave length of light and the angle of convergence of the rays at the extremities. For a fixed wave length, and for a constant diameter of the base of the bundle of rays, the width of the image varies with the focal length. But since the size of the elementary disks varies noticeably in the same ratio, the result is that the number of different parts does not change. Because of this sort of logic, we have been led to construct short-focal-length telescopes without fear of affecting their optical power.
But if this optical power only depends on the useful surface of the objective, then one should expect that in reducing the active surface of a good mirror by using a diaphragm or stop, one should reduce the optical effects of the mirror in proportion. This result, which was foreseen, seemed to be so contrary to what ordinarily occurs that it seemed wise to us to check it directly.
This experiment has been repeated several times on telescopes of all sizes, and it has now been confirmed that by local refiguring one can bring mirrors to such a degree of perfection that they cannot be subjected to any diaphragm or stop without losing some of their optical power. From this flows a new character and a very simple test that can be used to check the quality of a telescope; for depending on whether they gain or lose in optical quality as they are stopped down, we can judge in a decisive manner how nearly they approach perfection.
All of these facts are additional confirmations in favor of the wave theory of light. In the former theory, the focus is simply the point where independent rays cross each other; the more rays, the brighter it is, but the smaller the probability that this crossing will occur at a unique point. But according to wave theory, the focus that forms in a homogeneous medium is the center of spherical waves with the same phase; the longer the wave length, the better this center is determined. The rays we consider geometrically have no individual existence; they are simply the direction of propagation of waves. Among these supposed rays that a surface is supposed to regroup at a focus, all are special: those that vibrate in phase constitute a limited focus; those that because of a surface imperfection have undergone a difference in travel path that incapable of putting them out of phase, are pushed a certain distance away from the others without ever being able to come closer to them than a certain limit. There is a discontinuity between the waves that are in phase and those that are out of phase, and this discontinuity reveals itself by the presence of a black circle that stands like a rampart around the large center of the effective rays. However, if by refiguring one is able to bring back those deviated rays, one will find that they will never penetrate that dark space; they avoid it and cross it as the effect of an unstable equilibrium, only to reunite themselves by pressing themselves against the group of in-phase rays.
This discontinuity in the path of the rays that are called upon to become effective, explains a phenomenon whose singularity has often struck us. When a surface, even a very incorrect one, is merely one of revolution, the phenomenon that one notices during the various focusing maneuvers consists in the fact that, in a greater or smaller area on either side of the point of best focus, one notices the presence of an image that remains clear, while still detaching itself on a background of ambient light. Assuredly, if the deviated rays could approach the focus closer and closer, this phenomenon would not appear, given that the successive foci formed by the different zones are continuously linked one to the next. But since in reality every focus is limited and essentially preserved from the confusion by a black annulus, whatever zone forms an image in the plane being observed in, is bounded on either side by inactive zones which assure to their own images the ability to dominate over the lighted background formed by the brusque dissemination of other rays.
The same explanation accounts for the phenomenon of doubling which occurs so frequently with large instruments. Opticians assume that doubling of images is due to an accident in their work which divides the surface of the objective into two discontinuous regions separated by a "parting" ridge. This explanation has no foundation, because one never finds an intersection between two regions, nor any surface discontinuity. In reality, image doubling is a result of the superposition in the converging apparatus of two distinct defects. It happens every time that the objective is marred with a positive or negative general aberration and also presents two central rectangular sections with unequal curvatures. We have discovered, when discussing the paths that have been followed, that in such a case there are formed in the converting ray pencil to excentric groups of active rays, and that the central rays that remain out of phase become inactive in their perpendicular direction. We can produce, at will, the phenomenon of image doubling by choosing a mirror affected by aberration and then compressing it along one of its diameters. When the aberration is positive, the doubling occurs perpendicular to the compressed diameter; if the aberration is negative, the doubling is parallel to that same diameter.
If we consider now that this ring surrounding the focal image of each point of light, and which works so powerfully to give definition to images, also has the effect of rejecting the rays that would harm the useful rays at a noticeable distance, then we can judge how much its presence must favor the application of our third method of examining optical surfaces. That method is precisely designed to establish how much those rays depart from one another, by the interposition of an opaque knife-edge screen.
When after doing refiguring all the harmful rays have returned into order, one can still not conclude, as we have already stated, that the reflecting surface has attained geometric perfection in all its rigor. However, the result is that the remaining defects are contained within limits which one can determine by very simple calculations. The formation of an exact focus implies the rigorous concordance or the absolute equality of the paths traveled by all of the rays. If a focus forms that appears perfect, it is not exaggerating to say that all the rays are in phase to at most one-half wave length, because those that were out of phase by any more than that would be rejected outside the first black ring, and would end up reinforcing the exterior rings. Now the average wave-length of light is about half of a thousandth of a millimeter, and a half-wavelength is a quarter of a thousandth [ of a millimeter]. But if any part of the surface is in error by a certain amount, then this error will act upon the paths traveled, whereupon it will be doubled by reflection. And since we have assumed that all of the rays are in step by less than one-half wavelength, it results that all the points on the actual physical surface of the mirror approach the theoretical surface by less than one eight-thousandth of a millimeter, or roughly one ten-thousandth of a millimeter.
Independent of the size of the surfaces, that is the degree of perfection which comprises local refiguring pushed to the point where we realize foci that are physically perfect. If we use the spherometer to test quantities of this order, it can only respond with uncertainty; how then can any machine working the glass attain them? We must therefore work by hand. But even the human hand cannot work alone; it must constantly be guided by the hints from the light itself.
To sum up, in this section, devoted specially to optical power, we have established that there is a group of characters by which one can tell that a surface approaches perfection. When such surfaces are subjected to examination, they cease to show any perceptible defects. The images they give take on a good appearance that is maintained under very strong enlargement, the contours are clear and can be seen accompanied by pale diffraction fringes. Also, when one applies a diaphragm stop, one notices that no portion of the objective can be masked off without a comparable weakening of the optical effects.
In order to give a numerical value to the concept of optical power, we consider it to be inversely proportional to the smallest angle under which one can observe the separation of the smallest details visible in the focus of an instrument. We took as our test subject a distant target formed by contiguous, alternating black and white spaces, placed at the limit of visibility on account of its distance from the telescope and the distances between the black and white areas. We expressed the optical power as the quotient of the distance from the target to the focal point of the telescope, divided by the mean separation between homologous sections in the target.
After a large number of experiments performed on mirrors and lenses of all sizes and focal lengths, we have determined that the optical power depends only on the diameter of the effective surface. Consequently, this power and this diameter are in a constant ratio characteristic of white light, and which expresses in a general way the delicacy of the agent or its virtual power of separation.
If we take the millimeter as our unit of length, to which the wavelength of light is normally linked, we find that this optical power is a number approximately equal to 1500. From this, we can deduce by a simple proportion the maximum optical power of any objective of any size.
We insist that there does really exist an absolute limiting power, so as to establish that which one should be able to expect from a telescope of any given size, and also to deter manufacturers from claiming to have obtained or trying to obtain optical results that are simply impossible.
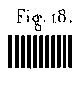 To judge the result with certainty, and to express those results in a form less vague than one normally uses in ordinary language, we should mount the mirror in a Newtonian telescope and aim it at a distant target. We should arrange this target is as to provide details placed at the limit of visibility. We construct these test targets by inscribing on a sheet of ivory a series of divisions arranged into successive groups, where the millimeter is divided into smaller and smaller parts. The thickness of the lines engraved should vary from one group to the next in such a way that the darkened portion has the same area as the interval that separates them (figure 18). If one views such a target placed at a distance, or if one observes it with too weak an optical instrument, then the different groups appear merely to have a uniform light gray color. But if one decreases the distance or uses more powerful optics, one sees that the groups that are the farthest apart resolve themselves into distinct lines, while the rest remain blurred.
To judge the result with certainty, and to express those results in a form less vague than one normally uses in ordinary language, we should mount the mirror in a Newtonian telescope and aim it at a distant target. We should arrange this target is as to provide details placed at the limit of visibility. We construct these test targets by inscribing on a sheet of ivory a series of divisions arranged into successive groups, where the millimeter is divided into smaller and smaller parts. The thickness of the lines engraved should vary from one group to the next in such a way that the darkened portion has the same area as the interval that separates them (figure 18). If one views such a target placed at a distance, or if one observes it with too weak an optical instrument, then the different groups appear merely to have a uniform light gray color. But if one decreases the distance or uses more powerful optics, one sees that the groups that are the farthest apart resolve themselves into distinct lines, while the rest remain blurred.