John M. Pierce's HobbyGraph Articles
HobbyGraf #4
Making Flats.
The magazine article #8, Making Flats, is quite apparently a rework from this article with some different images and a bit more organization.
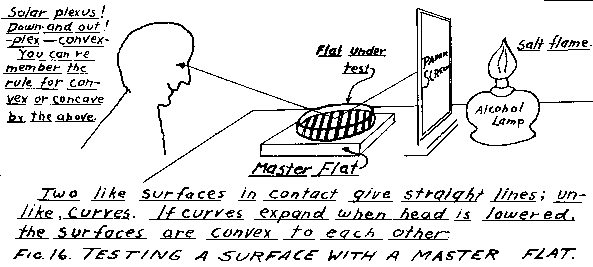The simplest way of testing the flatness of a surface is to compare it with a master flat. This is the best way. You use the principle of interference of monochromatic light such as is given by a salt flame. The master flat is laid, flat side up, on a piece of black paper or cloth. The piece to be tested is laid, face down, on the master, and they are illuminated by light from an alcohol lamp. Salt is rubbed on the wick to make it give a yellow sodium light used in testing. A screen of tracing paper is placed between the lamp and the glasses to give a sizable area of diffused monochromatic light. Now observe the reflection of this screen in the glass being tested. If the glasses are in close contact a series of yellow and black interference lines will be seen. These indicate how the two surfaces match. The top surface of the master and the bottom surface being tested produce the lines. Press one edge of the glass until the lines run across the glass as in Fig. 17. Lay a straight edge across, connecting the two ends of a dark line and count the light lines between this dark line and the ruler. Each line represents a difference in the space between the glasses of about .00001". In Fig. 17 there are 1 1/2 lines showing that, if the master flat is correct, the glass being tested is .000015" convex or concave along the chord represented by the straight edge. Now move the head down vertically. Watch the interference bands. If these appear to move out from their center of curvature the curvature of the surface is convex, while if they move in it is concave. This is most apparent if the glasses are pressed to make the bands circular rather than arcs approaching a straight line.
A master flat sufficiently accurate for small work such as plano lenses and diagonal mirrors can be selected from a piece of plate glass as follows: - Secure some plate glass of good quality. A broken mirror, or windshield (not safety glass). Cut it into 2" squares. Test A on B, A on C, and B on C. These three surfaces are flat and the back of each should be marked with a glass cutter to identify them. The small diagonal mirror for a Newtonian telescope can frequently be selected from a piece of plate glass by going over it with a master flat, testing it in various places until a flat spot is found, as shown by straight interference lines, and there cutting out your diagonal.
To make large flats procure three discs of plate glass or Pyrex of the size desired. Use Pyrex for flats over 8" if possible as it does not scratch so easily and changes less with a change of temperature. Thickness should be at least 1/8 of the diameter. Mark these on the backs A, B, C. Then grind these together in all combinations, A and B, A and C, and B and C. Reverse frequently so no disk will remain top or bottom too long with resulting curvature. If polished plate is used only the finest grit will be needed simplifying matters greatly. Grind only long enough to give a good fine ground surface and then polish on a pitch lap. One hour's polish on each of the three will be sufficient. After testing the one most nearly flat will be finished, the others being used for the checking of the one chosen.
Test all combinations of the three worked surfaces with the salt flame as in Fig. 17. Then form three algebraic equations.
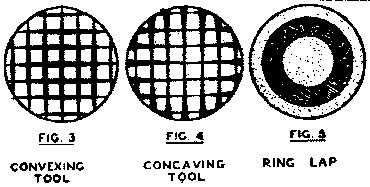First half of each equation is expressed as the sum of the two flats under test as A plus B, A plus C, etc. The last half of each equation is the number of bands by which the surfaces are convex to one another and the negative if they test concave. We will suppose our tests show with A on B 6 lines between the curved lines and the ruler, and that they expand as we lower our head. Our equation is then A plus B equals 6. We will suppose when A and C are tested we get A plus C equal 2, and with B and C we get -1. We solve these equations algebraically and get A equals 4, which means that the A is 4 fringes or .00004" convex from a perfect flat. B works out to be 1 and C to be -2 or .00002" concave. If only one flat is to be finished we will select B as being the nearest flat, and trim our lap like Fig. 19, as we want to polish away mostly at the center to cut down our convex surface and change it to a flat. If the disc selected had been concave we would have trimmed our lap like Fig. 18. Test frequently and when your equations give a zero value for B you are done. If while testing one flat is moved on another, inequalities in it will move with it. In this way a turned edge of zonal irregularities may be detected. There is usually a slight turned down edge but if the lap is made slightly smaller than the flat this tendency is reduced. In making a flat the same problems come up as in making a mirror and are met in the same way.
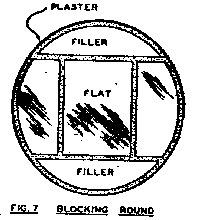
Small rectangular flats or prism faces are blocked out with pieces of glass to give a round shape and are held in plaster of paris while grinding and polishing. Lay face down on a piece of glass and arrange the blocking, leaving about 1 1/16" of space between pieces. Place a bottomless tin can around them and pour in an inch or more of plaster. When set remove the can and slip from the glass underneath, and with a knife clear away the plaster between the pieces of glass and around them 1/16" deep, and paint with melted wax to protect from water. Fine grind on a piece of plate glass. Polish by hand or, if small, on a vertical spindle like a lens. Fig. 20 shows a rectangular piece blocked up for polishing. The round shape is necessary as without it the corners would certainly be turned down.
Optical glass prism blanks may be ground to shape by hand on a piece of plate glass, using a square and protractor to obtain the correct angles. It is very difficult for a beginner to make a good prism, and it is much better to use a flat diagonal mirror unless a really good prism can be purchased. Beware of prism bargains. A poor prism is worthless for our purposes.