 |
 |
Many amateur telescope makers who have tried to use their telescope on terrestrial objects have been puzzled by noticing that the focal point for fairly near objects is not the same as for the stars and planets. Possibly they were not even to pull the eyepiece enough to focus on nearby objects.
The telescope, like the camera, requires a longer extension for near than for far objects. Stars and planets, however, all have the same focus because they are all distant objects. The focal length of a mirror for distant objects is equal to half its radius of curvature. To find the position of the focal points for nearer objects we must use the law of conjugate foci (given at the end of this article), which applies equally to mirrors or lenses.
We will consider a mirror of 100 inch radius of curvature. This give a value of F of 48 inches (note: John Pierce made an error here as the real number is 50 inches) or 4 feet. If we observe an object at 25 ft., 100 ft., 1000 ft.. and infinity, and mote the different focal distances, we find that, for objects as near as 25 ft., the eyepiece has to be extended as much as 0.76 ft., or about 9 inches farther than for the stars. Objects 100 ft. distant require an extension of 0.17 ft. or about 2 inches; while objects 1000 ft. away require an extension of about 0.2 of an inch.
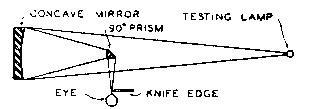
Objects nearer than 25 ft. will require still longer extension. The focus for an object at 96 inches (2F) (note: again an error between focal length and radius of curvature) is at this same distance (96 inches). This condition is fulfilled when we test a mirror at it's center of curvature with a lamp and a knife-edge. An object at the primary focus has its focal point at infinity; the rays from the objective lens or mirror being parallel rays that meet only at an infinite distance. Objects nearer than the primary focus have no real focal point, the rays form the lens or mirror being diverging rays.
A 10 inch telescope should show stars of the 14th magnitude; a 16 inch those of the 15th magnitude, and to see 16th magnitude stars requires a telescope of 24 inches aperture. Of course this applies to stars that we can see visually with the telescope. Much fainter stars can be photographed, the limit for any given telescope depending upon the length of photographic exposure.
The stars cross our sky at the rate of 360 degrees in 24 hours, or 15 seconds of arc, in one second of time. To find the actual angular aperture of a telescope with a certain eyepiece, time the passage of the star across the field of view; then multiply this time in seconds by 15 which will give the aperture of the telescope in seconds of arc.
For example, suppose we time the passage of a star, from the time it first appears on one side of the eyepiece, until it disappears on the opposite side and find it 47 seconds; 15 x 47 seconds is 705 seconds or 11 3/4 minutes of arc.
To find the apparent angular aperture multiply this by the power of the telescope. Suppose this was 48 inch focus mirror used with a 1/2 inch eyepiece; the power would be 48 divided by 1/2 or 96x. The apparent aperture then would be 95 x 11 3/4 arcminutes or 1128 arcminutes or 18.8 degrees.
Formula for Conjugate Foci: 1/F = 1/f + 1/f' where F = focal distance for distant objects = 1/2 radius of curvature f = Distance from lens or mirror to object f' = distance from lens or mirror to the image formed.A larger telescope magnifies distances, but not the apparent diameter of stars.
Method of testing a telescope mirror; see previous articles for fuller instructions.
 |
 |