 Testing glass surfaces by interference bands of light. The master flat is under the flat to be tested. The alcohol flame is monochromatic yellow produce by rubbing salt into the wick. Two like surfaces in contact, will give straight lines.
Testing glass surfaces by interference bands of light. The master flat is under the flat to be tested. The alcohol flame is monochromatic yellow produce by rubbing salt into the wick. Two like surfaces in contact, will give straight lines.Optical flat are use in testing the plane surfaces of lenses, prisms or mirrors. They are also used as part of telescopes, and in setups where an image is to be reflected without distortion. The ordinary type of reflecting telescope, the Newtonian, uses a diagonal mirror or a prism near the focal plane of the mirror to throw the image to the side of the telescope, so that it will be in a convenient position for magnification by the eyepiece.
A large flat is needed in making a Cassegrainian telescope (which has certain decided advantages over the simpler Newtonian). A future article will deal with the Cassegrain and also with this method of testing.
Even in testing the parabolic mirror, a large flat may be used to advantage, giving results much more accurate and easily interpreted than those obtained by the ordinary way of testing at the center of curvature of the mirror. (Part 2 of this series of articles.) No matter what method of testing and figuring a flat you may decide to use, the methods of grinding and polishing are alike; and they will be described before attempting the more difficult operations.
Blanks for the flats and tools are to be of polished plate glass. The flats should be, in thickness, at least 1/6th of their diameter. The tools may be thinner but not less than 1/8th. Blank and tool are ground together, using only the finest grad of abrasive. Grinding is carried on exactly as in grinding the telescope mirror (Part 1); except that two piece of glass are reversed in position frequently, one on top and then the other. This is to avoid the tendency of the upper piece to become concave - highly desirable in making a concave mirror but fatal if allowed in a flat. Grinding is continued only until the polished surface of the glass is ground all over; the least amount possible is best, since the original surface was probably accurate to within .001 inch, and we can easily grind it much worse than this.
We then make an ordinary pitch lap as described in Part 1 (Sept., 1933) and polish, using a short stroke, for about half an hour. By this time the surface is polished enough to give a reflection, so that testing can begin, and the changes in polishing procedure necessary to make the flat surface can be carried out.
The simplest method of producing an optical flat is to copy a master flat, if one is obtainable. To test, the master is placed on a piece of black paper or cloth, face up as shown in Fig. 1, in front of a monochromatic (single colored) light source. The ordinary way of obtaining monochromatic is to rub common salt into the wick of an alcohol lamp; this gives a brilliant yellow light that works beautifully. A neon light, such as used in signs, is also suitable, or the Cooper-Hewitt mercury vapor light.
 Testing glass surfaces by interference bands of light. The master flat is under the flat to be tested. The alcohol flame is monochromatic yellow produce by rubbing salt into the wick. Two like surfaces in contact, will give straight lines.
Testing glass surfaces by interference bands of light. The master flat is under the flat to be tested. The alcohol flame is monochromatic yellow produce by rubbing salt into the wick. Two like surfaces in contact, will give straight lines.
A diffusing screen of ground glass or tracing paper is place in front of the light, to give a large illuminated area. Your semi-polished disc is now placed face down on the master flat and pressed into close contact with it. If observed as in Fig. 1, looking at the reflection of the screen in the blank, you should see a series of colored interference bands or fringes. Press one edge of the disc of glass until the bands run across the glass and are about 1/4 inch wide.
CAUTION: Be sure that both glass surface are clean; or scratches will result from the pressing and rubbing necessary to get the interference fringes into the position desired.
 Method of counting fringes with the aid of a straightedge.
Method of counting fringes with the aid of a straightedge.
Lay a straightedge or scale across the discs of glass, as in Fig. 2, from end to end of the same fringe, and count the number of fringes cut by the straightedge. A fringe consists of a dark and a light band; and each fringe consisted of a dark and light band; and each fringe represents a difference in the space, between the two glasses, of half a wavelength of the monochromatic light used. If you are using a salt flame or a sodium light, each fringe is about .00001 inch. In Fig. 2, this is about 1 1/2 fringes or .000015 inch. In other words, if the master flat is perfectly flat the blank is .000015 inch concave or convex, and we must modify our method of polishing to change this to the flat surface desired. To do this we have to know ;whether our surface is concave or convex. This is easily done by pressing the edge of the glass toward the center of curvature of the interference bands - bottom edge in Fig. 2 - and noting whether the bands move toward your finger or away from it. If they move toward the point of pressure, the disc is convex; but if they move in the opposite direction - away from your finger - the disc is concave. Another method of telling whether the surface is convex or concave is to press the glass until the fringes become circles. Then standing as in Fig. 1, lower the head vertically and not whether the circular fringes appear to expand and move out from the center in which case the surface is convex; or become smaller in size, moving toward the center, in which event they are concave.
If our disc is only slightly convex, say one or two fringes, we can wear away the central faster than the edge, thus flattening it, by using a long stroke with the mirror on top of the lap. Experiment only will show just how long a stroke to use. If too long, the center will polish out too fast, producing a hollow center. Try a stroke about half the diameter in length, and test frequently, changing the length as the results indicate. If the surface should be slightly concave, place the mirror underneath, polishing with the lap held in the hand. In this case, however, it is essential that the workman move entirely around the flat when polishing, and not just back and forth around a corner of the workbench (which is allowable when the mirror or flat is held in the hand and so completely revolved in that manner). Otherwise we will produce an astigmatic or saddle-backed flat.
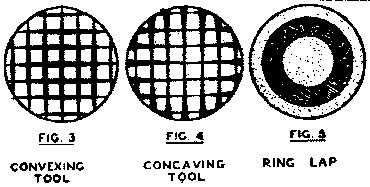 If the imperfection of the surface amounts to more than three fringes, it is usually best to modify the lap by widening the grooves gradually from the edge to the center or vice versa. This reduces the area of the lap over the low areas of the flat, making those areas wear away more slowly than others, and tending to flatten the surface. Fig. 3 shows a lap with its center facets reduced in size for polishing a concave surface, and Fig 4 is the reverse, center facets largest for flattening a convex surface. These modified laps are usually place on the bench with the work in the hand, and a short stroke (one fourth the diameter) is used. Frequent testing is necessary; and such further modifications of the lap, or the return to the original normal lap, are carried out as the changing surface demands.
The lap should always be made slightly smaller than the surface being polished, to avoid a turned-down edge on the mirror. Trim off about t1/4 inch all around the edge, using a sharp knife; otherwise you will certainly have a useless edge. If, in spite of all precautions, you get a bad edge, you can grind it off or cover it up without shame, as many famous makers have done before you.
If the imperfection of the surface amounts to more than three fringes, it is usually best to modify the lap by widening the grooves gradually from the edge to the center or vice versa. This reduces the area of the lap over the low areas of the flat, making those areas wear away more slowly than others, and tending to flatten the surface. Fig. 3 shows a lap with its center facets reduced in size for polishing a concave surface, and Fig 4 is the reverse, center facets largest for flattening a convex surface. These modified laps are usually place on the bench with the work in the hand, and a short stroke (one fourth the diameter) is used. Frequent testing is necessary; and such further modifications of the lap, or the return to the original normal lap, are carried out as the changing surface demands.
The lap should always be made slightly smaller than the surface being polished, to avoid a turned-down edge on the mirror. Trim off about t1/4 inch all around the edge, using a sharp knife; otherwise you will certainly have a useless edge. If, in spite of all precautions, you get a bad edge, you can grind it off or cover it up without shame, as many famous makers have done before you.
Be sure to place the lap in hot water for a minute, before starting work each day. Then the first few polishing strokes produce perfect contact. Cold pressing with the master flat is also valuable. Place the master on the lap at room temperature; weight it with about 10lb.; and leave for thirty minutes. Paint the flat with thin polishing rough, so that it will not stick. If fairly hard pitch is used, there is less danger from a turned edge or zonal errors.
Raised or depressed zones may be detected by irregularities in the interference bands, but they are much easier to discover by the reflection method of testing, which will be described later on in this article. They will rarely appear if good contact is maintained. A raised zone may be polished down with the ring lap - Fig. 5 - the ring being just the size of the raised zone. For a depressed zone, the ring is cut away, leaving the rest of the lap to do the work. A ring lap need not be cut into facets. Simply form the lap with the flat, scribe two circles, for the inside and outside of the ring, with a compass, and cut away with a knife, the surface of all the lap except the ring for a depth of about 1/16 inch. Very short strokes are used with both of these laps - not over an inch long. they work very rapidly, and testing every 50 strokes is advised. When the zone is removed, small irregularities are usually left. These may be smoothed away by returning to the full sized normal lap.
Usually, the amateur telescope maker has no master flat to guide him. In this case there are two methods of making an original flat, either of which is within the ability of the average amateur.
The first to be describe will be a modification of the machine shop method of producing a flat surface metal plate. Three surfaces are prepared by machining as flat as possible, and then coating with a very thin coat of red lead or Prussian blue, and rubbed together in all combinations: No. 1 with No. 2: No. 1 with No. 3 and No. 2 with No. 3. The spots that touch are indicated by the paint. These spots are scraped, testing and scraping being continued until all three surface touch each other over their whole surface to the accuracy required. If the three surfaces touch all over, in all three combination, it is apparent that they must be flat. In applying this method to producing a glass flat we use three glass discs' but we flatten only one of them, thus reducing the labor considerably. Besides the three disc for the flats, we will need several others to serve as bases for the several laps we will use in producing our flat (unless we have stove lids, or other iron discs we can use them as bases). Mark the three glass disc A, B, and C on the back with a glass cutter. These discs are ground in short periods A on B, A on C and B on C, using the finest grit only, and then are given a semi-polish, as has been described. They are then tested with the monochromatic light, by placing them together in pairs and noting their interference bands. From these observations the curvature of each surface is determined mathematically.
Another method is making a flat by algebra. If algebra was one of your weak subjects you needn't worry, for only the simplest of algebra is used - the solution of three simple linear equations. First place disc A on disc B, semipolished surfaces together, before the screen as in Fig. 1. Using a straightedge as in Fig. 2, could the fringes showing the difference between the two surfaces as explained before. Now form an algebraic equation, the first part being the sum of the two flats tested, as A+B, and the last part the number of fringes. Convex is + and concave -. Do the same with flats A and C, and B and C. Suppose that, when A was on B, we counted 5 fringes cut by the straightedge and the surfaces were convex to each other, as shown by the fringes moving toward the finger when the discs were pressed together at the edge, as before described. This equation would be A+B=5. We will also suppose that A on C gave 2 fringes convex, and B on C gave 1 fringe concave. Our three equations then would be:
| A | +B | =5 | ||
| A | +C | =2, | ||
| B | +C | =-1. | ||
| Solving for A, B and C, we find: | ||||
| A | +B | =5 | ||
| A | +C | =2 | ||
| ________________ | ||||
| Subtract | B | -C | =3 | |
| B | +C | =-1 | ||
| ________________ | ||||
| Add | 2B | =2 | ||
| B | =1 | = 1 fringe convex | ||
| Substitute | 1 | +C | =-1 | |
| C | =-2 | =2 fringes concave | ||
| A | +1 | =5 | ||
| A | =4 | =4 fringes convex | ||
This indicates that surface A is 4 fringes or about .00004" convex from a perfect flat; B is 1 fringe or .00001" convex and C is -2 fringes concave or .00002" concave.
Since only one flat is to be made, we select flat B as being nearest perfect, and reserving the other tow for testing, we proceed as before explained to polish away that one fringe of convexity. Test frequently, and he you equations solve, giving B equal to 0, the mirror is flat. Don't attempt to get the surface too perfect before it is completely polished; as you would probably spoil it if you continued to polish after perfection had been reached.
If, in testing, zonal irregularities are seen, slide the top disc on the lower. If the imperfection is in the top glass, it will move with this but, if in the bottom, it will remain stationary. Choose for finishing a disc without zonal defects, even if further from flatness; as simple curvature is easier to correct than a bad zone. For the same reason, choose a convex surface rather than a concave one.
A small flat suitable for the diagonal of a Newtonian telescope can frequently be picked out from a number of pieces of glass cut from broken windshields, mirrors, etc. A six inch telescope would require one about 1 inch by 1 1/2 inch. Pieces of this size are marked for identification with a crayon, and then tested in groups of three as above; the flatness of each piece being determined algebraically and marked on the glass, and then the best is selected for use as a diagonal mirror.
An error not in excess of one fringe, whether concave or convex, will usually work satisfactorily if the diagonal is not placed further from the eyepiece than 5 inches, when used with a 6 inch mirror of 50 inch focal length. The second way of producing an original flat was suggested some years ago by Professor Ritchey in "The Modern Reflecting Telescope" (a book long out of print). In this method a spherical concave mirror at least as large as the flat is first made and figured to give a unfortunately shaded surface when the knifeedge is cut into the cone of rays at the center of curvature. See Part 2 of this series of articles, or the book "Amateur Telescope Making." This spherical mirror is silvered and set up as shown in Fig. 6 with the flat close to it and at 45 degrees with it, and reflecting the cones of rays from the testing lamp and Knife-edge.
If the flat is perfect, there will be no change in the appearance of the concave mirror from tests made in the ordinary way at the center of curvature. Zonal irregularities will, however, show up very strongly; sine the zone acts on the light twice - first as it comes from the lamp, and also on its way back to the knife-edge and eye, after reflection by the concave surface.
If the flat is concave or convex, this fact will impress itself on the cone of rays, lengthening or shortening the focus for those rays which fall on edges A and B as opposite ends of the horizontal diameter; those rays coming from the top and bottom edges C and D are not so affected. To interpret this condition, we must arrange our knife-edge to slide up and down, as well as sideways. Cover all the flat except the top and bottom edges; and then adjust the knife-edge so that, when the cone of rays is cut vertically, both top and bottom darken at the same time. Then mark this position with a pencil on the table or support. Mark all but the two horizontal edges and side, place where both sides of the mirror darken simultaneously and mark this place. Should this coincide with the mark obtained for the vertical movement, the flat is really flat. If the horizontal mark is nearer the mirror than the vertical mark, the flat is concave, and should be worked on a tool like Fig. 3. If the horizontal mark is further away from the mirror than the vertical mark, the flat is convex; and a tool like Fig. 4 should be used. This method of testing a flat is probably more accurate than any other, especially for detecting zonal faults.
 The small flat for a diagonal mirror can be tested by this method in connection with it's parabolic mirror. Place the flat close to the center of the parabolic mirror, as at 45 degrees to it. This will work well for a small flat, as the central portion of a parabolic mirror appears under test to be spherical because of the very small aperture of the central part which we are using. Suppose we have a 6 inch mirror of 48 inch focus; this is an aperture of F-8. If we use only the central 2 inches in our test, it would be F-24, which would appear perfectly spherical to most observers. If only the central 1 1/2 inch were used, it would be a F-32, the parabolic shadow of which is probably beyond the detection of even the most experienced worker.
The small flat for a diagonal mirror can be tested by this method in connection with it's parabolic mirror. Place the flat close to the center of the parabolic mirror, as at 45 degrees to it. This will work well for a small flat, as the central portion of a parabolic mirror appears under test to be spherical because of the very small aperture of the central part which we are using. Suppose we have a 6 inch mirror of 48 inch focus; this is an aperture of F-8. If we use only the central 2 inches in our test, it would be F-24, which would appear perfectly spherical to most observers. If only the central 1 1/2 inch were used, it would be a F-32, the parabolic shadow of which is probably beyond the detection of even the most experienced worker.
Frequently a flat is made at the same time as a parabolic mirror by using three glass blanks; on for the mirror, one for the flat and one for a tool. First the mirror is ground over one side of the too, a lap made, and the mirror corrected to a true spherical curve. This is usually not difficult, as the spherical curve is the natural one to obtain in polishing. Next the flat is ground on the other side of the tool, a new lap made and it is polished and figured, using the spherical mirror, by the reflection method. The lap is reformed to the mirror's curve, and the spherical mirror is parabolized; either by testing at the center of curvature, as before described, or by a more rigid test, using the large flat. This method will be explained in a later article of this series.
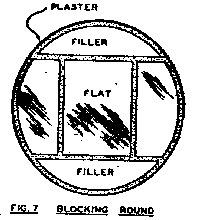 A flat should always be worked in a round shape and then this shape modified, as desired, to elliptical or rectangular form. Small rectangular flats or prism faces are blocked out with pieces of glass, as shown in Fig. 7, to give a round shape. These are bedded in plaster of Paris as follows: lay the pieces of glass face down on a piece of plate glass leaving about 1/8 inch between the pieces. Place a bottomless section of tin can around them, and block up the edges of the can with strips of pasteboard or matches to leave a little space below it. Pour in an inch or more of the plaster; when set, remove from the plate glass and dig out the plaster around the pieces of glass for a depth of an eighth of an inch.
A flat should always be worked in a round shape and then this shape modified, as desired, to elliptical or rectangular form. Small rectangular flats or prism faces are blocked out with pieces of glass, as shown in Fig. 7, to give a round shape. These are bedded in plaster of Paris as follows: lay the pieces of glass face down on a piece of plate glass leaving about 1/8 inch between the pieces. Place a bottomless section of tin can around them, and block up the edges of the can with strips of pasteboard or matches to leave a little space below it. Pour in an inch or more of the plaster; when set, remove from the plate glass and dig out the plaster around the pieces of glass for a depth of an eighth of an inch.
Later cover all the plaster surface with melted paraffin or beeswax, to protect it from water in grinding and polishing; fine grind on a piece of plate glass and polish by hand in the customary manner on a pitch lap. Small jobs may be ground and polished on a rotating lap, such as used for grinding and polishing small lenses - Part 4.
It is very difficult for a beginner to make a good prism. Making the flat surfaces is not too hard; but to get the 90 degree angle much better than a cheap prism. A good prism however is preferable to a flat on a small refractor - up to 12 inches aperture - because the light lost by absorption in passing through the prism is less than that lost by reflection at the silvered surface of the flat, especially when the silver becomes somewhat tarnished. Larger telescopes than 12 inch, however, should have the diagonal flat, because the large prisms for these absorb a greater amount of light.