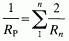 ;
(1)
;
(1)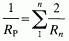 ;
(1)
;
(1)
R1 = -2F; R2 = 2(1-x)F; R3 = -2xF (2)
and the condition for a flat focal surface (equation (1) above) becomes:
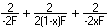 (3)
(3)
which may be simplified to:
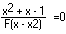 (4)
(4)
The solutions to the quadratic equation in the numerator of the equation (4) are:
x = -1.618034 and x = +0.618034(5)
Some readers will notice that the number 1.618034 is the Golden Section Ratio, commonly denoted by r, which was known to the ancient Greeks and occurs in a number of geometrical contexts including the limiting ratio of the terms in the Fibonacci Series (Coxeter 1940); it also appears in the design of three-mirror systems in which spherical aberration is corrected with a paraboloidal primary and spherical secondary and tertiary mirror with non-parallel light between these (Rumsey 1971).
In order to retain the excellent, Schmidt-like performance the tertiary mirror should remain spherical (within the Seidel approximation), and, as noted above, it's center of curvature should coincide with the pole of the secondary. The light falling on it from the secondary should not be exactly parallel, as it would be for an axial object if the primary and secondary were for an axial object if the primary and secondary were both paraboloids, but the wavefronts should be distorted in the same way as by a Schmidt corrector. In the Paul system which has secondary and tertiary mirrors with numerically equal radii of curvature the spherical aberration of the tertiary mirror is corrected if the secondary is also spherical.
When these two mirrors have unequal radii, and the secondary has the shorter radius, as here, the spherical aberration of the tertiary mirror will be corrected if the secondary is an ellipsoid with suitable eccentricity. It was found by successive approximations that, if the primary is a paraboloid with a focal length of 8m and an aperture of 5m (as in the design in Paper 1), the Siedel spherical aberration of the system will be corrected with a secondary mirror having a radius of curvature R2 = 6.111456m and eccentricity e2 - 0.866 and the spherical tertiary mirror with R3 = 9,888544m.
The higher order spherical aberration was then corrected by applying figuring (mainly r6 and r8 but also a small adjustment in r4) to the secondary mirror, and coma and astigmatism were much reduced by figuring two of the mirrors at a time in such a way as to avoid degrading the axial images.
Some higher order astigmatism and curvature of field remainder, and this was corrected by increasing the r2 term in the power series defining the secondary mirror; note that as the higher terms were not changed, this is not the same as changing the curvature while keeping the eccentricity constant. This change reintroduced spherical aberration, which was removed by increasing the spacing between the primary and secondary mirrors.
The baffles required to prevent sky fog over the 3 º field cause an obstruction amounting to 33.7 % by area.
The construction details of the design are given in Table 1, the optical performance in Table 2 and spot diagrams of 11 images in Fig.2.