From the Monthly Notes of the Royal Astronomical Society (1984) Vol. 210 pp 597-609
The Mersenne-Schmidt: a three-mirror survey telescope. Accepted 1984 March 20, Received 1984 February 10.

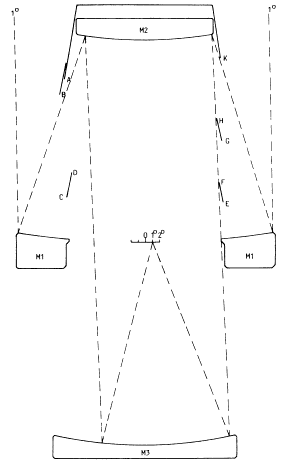
Figure 1. Optical arrangement of the Mersenne-Schmidt. The perforated primary mirror, M1 is approximately paraboloid, the convex secondary, M2 and the concave tertiary, M3, are approximately spherical. Dimensions and details of figuring are given in Table 2. On the left of this figure Baffle A is sufficient to shield the central 2º of diameter of the field from stray sky light reflected by the tertiary mirror. To shield the full 4º; diameter this baffle can be extended to B, or A can be used with the conical baffle CD. The obscuration can be reduced by the arrangement shown on the right of the diagram. For an explanation, see the text Section 3.2. The dimensions and locations of the baffles are given in Table 2.

      The design is shown in Fig. 1, and details are given in Table 1. It depends, like the Paul-Baker system, for its good optical performance on the properties of coaxial, confocal paraboloids first described by Mersenne (1636) and the principles of the Schmidt camera (Schmidt 1931). As the primary mirror is perforated in this design but not in the Paul-Baker systems, it is suggested that this should be known as the Mersenne-Schmidt. Three of Mersenne's diagrams, the upper and lower ones on his page 61 and the upper on page 62 have been reproduced in facsimile by Danjon and Couder (1935, their figs. 304a, b, c respectively) and first and last of these show a perforated concave paraboloid, used with confocal paraboloidal secondary mirrors, the first concave and later convex. Mersenne did not consider off-axis objects.

      Two sets of spot diagrams, for images on axis and at .2º, .4º ... 2º off axis, are shown in figs 2a and 2b, for two designs which use the same mirror spacings, apertures and axial curvatures, but different asphericities. The first of these gives diffraction-limited images on axis, 0.049 arcsec total (ray theoretical) image spread (0.23 arcsec rms diameter) at 1º off axis and 0.44 arcsec total image spread (0.263 arcsec rms) at 2º, or from the ground over 4º. The second design also has diffraction-limited images on axis, but is adjusted to improve the performance of 2º off axis, at some cost to the image quality at intermediate angles. The maximum image spread is 0.31 arcsec, 0.17 arcsec rms diameter. Details of the performance at intermediate angles are given in Table 2.

Figure 2. Spot diagrams for images in the Mersenne-Schmidt: (a) Version 1: (b) Version 2 (see Table 1). In each set, the top row shows images on axis and 1º and 2º off axis, the second row .6º and 1.4º off axis. The diameters of the circles are (a) 0.1 and 0.5 arcsec, (b) 0.4 arcsec.

      It may be of interest to record here the method by which the designs in Table 1 were reached. Initially the mirrors were strictly paraboloidal and spherical. This arrangement is corrected for Seidel spherical aberration, coma and astigmatism, but on axis higher order spherical aberratino leads to images 27.7 arcsec in diameter. This was corrected by making the secondary mirror aspheric, reducing the (ray theoretic) axial image spread to .0002 arcsec. The figuring required was a turned down edge, amounting to about 40um in the r₆ term, 3.4um in the r₈ and 0.3um in r₄. The image 1º off axis still suffered from coma and astigmatism, and was 3.9 arcsec (radially)x 2.1 arcsec. Coma was estimated from four rays in the principal plane, two at the edge of the aperture and two near the center, in the focused image; astigmatism was estimated from the distance along the axis between the image having least rms spread in the radial direction, and that with least tangential spread. These faults con be corrected by more figuring, if one of the mirrors is modified by changing the coefficient of r₁₀ in its description then the axial image can be restored to its previous quality by making a compensating change in the coefficient of r₈ in either of the other two mirrors. There are three possible pairs of mirrors that can be figured, each pair changes was estimated from the distance along the axis between the image having least rms spread in the radial direction, and that with least tangential spread. These faults can be corrected by more figuring, if some of the mirrors is modified by changing the coefficient of rn in its description then the axial image can be e restored to its previous quality by making a compensating change in the coefficient of rn in either of the other two mirrors. There are three possible pairs of mirrors that can be figured, each pair changes the coma and astigmatism in different proportions, but only two of these changes are independent. Nevertheless, this is enough to allow both coma and astigmatism, evaluated as described above, to be eliminated. In principle this can be done using the r₄, r₆ or higher terms in the power series, but a change in the r₄ term is equivalent to a change in eccentricities of the mirrors, and the system is already corrected in the Seidel approximations by using a paraboloid and two spheres. It is therefore logical to make the corrections by changes in the r₆ terms.

      It is notable that the r₆ figures used to remove coma that was estimated from rays at the ends and near the center of one diameter of the aperture, and astigmatism, also result in very small residual lateral ray displacements at intermediate points in the aperture. Further investigation showed that if the coma and astigmatism had been removed by applying r₈ figuring those residuals would have had roughly the same form, but with their signs reversed, and the residual would have been larger. It was clear that the images could be improved still further by making most of the correction of coma and astigmatism with the r₆ terms and a small part by the r₈ terms. Trial and error showed that 89% of r₆ and 11% of r₈ gave something near the best possible correction at all angles off axis up to 2º and reduced the image 1º off axis to 0.052x0.046 arcsec (total spread), 0.0227 arcsec (rms diameter). Rounding off the construction data caused some small changes in the image sizes. Automatic optimization of the optical performance by computer has not been used at any stage, if it were some further improvement of the images 1º off axis would be expected, while the images near the axis would be slightly degraded. A similar method was used to arrive at the second design, except that coma and astigmatism were removed at 2º off axis.

      The improvement which these two designs show compared with the Paul and Baker versions results from the use of the same basic principles (confocal paraboloids and Schmidt camera) and the acceptance of small but highly significant departures from the strictly paraboloidal primary and spherical tertiary mirrors used by Baker.

      Both of these designs are adjusted for use without a filter. When a filter of thickness t = 3mm and refractive index of n = 1.52 is inserted spherical aberration is introduced over the whole field of view, and coma off axis. The monochromatic image spread on axis is then 12um (0.3 arcsec at the present focal length of 8m). Fortunately the image quality can be restored approximately by changing only the separation of the mirrors. In Version 1 (2º field) the maximum ray-theoretic image spread is reduced to 0.044 arcsec by changing the mirror spacings to 3999.42mm and 8004.83mm; in Version 2 (4º field) spacings of 3999.40 and 8004.50mm result in a maximum spread of 0.323 arcsec, only 5% larger than with no filter. In white light there is also a defocusing effect amounting to t-delta(1/n); in order to keep the additional image spread from this cause under 2um (about 0.05 arcsec at 8m focal length) the range of foci should not exceed 6.4um at F/1.6 (if the focus is correct at the center of the passband). Passbands should then be kept under about 25nm at 390nm, 50nm at 500nm and 100nm at 650nm if the filter is 3mm thick and of a type of glass similar to Schott GG495.

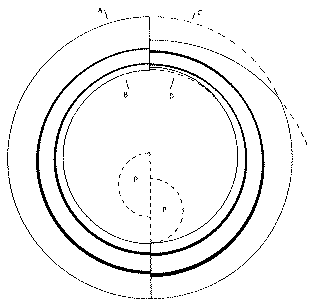Figure 3. Entrance pupils of the Mersenne-Schmidt with baffles as on the right of Fig. 1: at the left, 1º off axis, right, 2º. Along the line AB, the circles represent: the outer edge of the primary mirror; the obstruction in the converging light caused by baffle GH; the same for baffle EF; the shadow of the edge E on the primary mirror. Along CD (2º off axis): the outer edge of the primary mirror (dotted); the edge of the perforation in the primary mirror; the obstruction in the converging light caused by baffle GH; the same for EF; the shadow of baffle K on the primary mirror; the shadow of baffle E (dotted where this is within the shadow of K). A circular plateholder P covering 4º diameter is everywhere within the central shadow, but a square plateholder would cause a small additional loss of light near the edge of the field.

      The right-hand half of the figure shows an alternative method of shielding the whole field 4º in diameter. The diameter of the lower edge of the lower conical baffle, E, is sufficient to prevent light passing through the gap between this baffle and the mirror within 4º of the axis; its distance from the primary mirror was determined empirically. the lowest, EF, and central, GH, baffles, if extended, would each intersect the same circle as baffle CD. The length of each baffle must be limited to avoid obstructing the light between the second and third mirrors. The lower edges of the central, G, and upper, K, baffles have diameters small enough to cast no extra shadow on the primary mirror, from any object within 1º of the axis . The lowest baffle causes 37.75% obstruction of the incoming parallel light; in the converging light the lower and middle baffles obstruct the equivalent of 1.24% and 2.02% of the incoming light, giving a total obscuration of 41.01%. this is little more than is caused by the single baffle around the secondary mirror which shields only the central 2º diameter of the focal surface. This gain is made at the cost of permanently obstructing two narrow annuli of the aperture. The entrance pupil of the telescope when fitted with baffles EF, GH and K as shown in Fig. 3 for objects 1º and 2º off axis. Diffraction effects might be expected, but in the case of the similar system of baffles on the Irenee DuPont telescope (Bowen and Vaughan 1973) these effects are reported to be unobtrusive. The central obstruction is much larger than is normally accepted in an astronomical telescope. However, it is not as great as the effective loss imposed on the 72 inch mirror of the Palomar or UK Schmidt telescopes by the use of a corrector with a clear aperture of 49.5 inch (52.7%).

Table 3. Sky fog baffles. Dimensions in mm.

Baffle	Function	Radius	Height	Height
			Outside	Inside
A	Shields central 2º diameter	1595	1589	3235
B	Shields 4º diameter	1685	1679	2935
C	With A, shields 4º	1550	1537	900
D		1451	1438	1400
E	Together, baffles E-K shield	1536	1523	800
F	A field 4º in diameter	1459	1446	1200
G		1407	1399	2470
K		1480	1470	3650
Notes. Data are rounded to the nearest mm. The thickness of the baffles is assumed to be 0.5 inch (13mm) except the edges of baffles A, B and K which are 0.25 inch (6mm). Radii are measure form the optical axis of the telescope, and heights above the pol of the primary mirror. For further explanation see the text, Section 3.