Calculation, Setup and Operation of the Hindle Sphere Test.
Here's a start on the Hindle Test Procedure
The Hindle Sphere Test is a testing setup for convex optics which allows for the null testing of a convex surface at a real focus so that the tests like the Foucault Test and the Ronchi Test can be done.
The test requires a perforated sphere which is called a Hindle Sphere to do the test.
The sphere required to be a good spherical surface of spherical shape and usually needs to be of a short focal length in order to be able to test the convex surface fully.
 The first thing to do is to figure out what you are doing as related to how big the convex surface is that you are going to test and it's various focii.
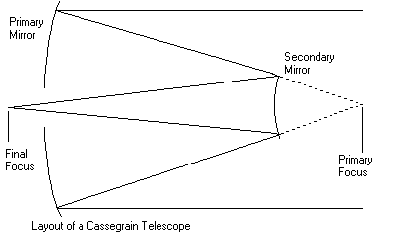
What I am interested in here is the testing for a hyperbolic surface for the Cassegrain telescope.
The secondary of a Cassegrain telescope is usually a hyperbolic surface of some pair of focii.
The near focus is behind the surface (on the concave side) and the far focus is on the front side of the surface.
You need to know both of these focii in order to be able to test the surface.
The first thing to do is to figure out what you are doing as related to how big the convex surface is that you are going to test and it's various focii.
What I am interested in here is the testing for a hyperbolic surface for the Cassegrain telescope.
The secondary of a Cassegrain telescope is usually a hyperbolic surface of some pair of focii.
The near focus is behind the surface (on the concave side) and the far focus is on the front side of the surface.
You need to know both of these focii in order to be able to test the surface.
There are a number of formulas used for deterring what the surfaces of a Cassegrain telescope are like that will be needed for the testing and let's review them now.
The distance to the focus of the system which is given as:
b = p (A + 1) - f
The magnification ratio of the secondary is given as:
A = p' / p
The ROC of the secondary is given as:
R = 2 * p * p' / (p' - p)
The (virtual) near focus of the secondary is the following:
p = (f + b) / (A + 1)
And finally, the Conic Constant of the secondary is given as:
SCC = - [ (A + 1) / (A - 1) ] 2
Where the following variables are these:
"p" = the virtual near focal point of the Cass secondary vertex (the rear point). This is where rays from the paraboloidal primary would focus if they were not intercepted by the secondary. This is also where the Hindle sphere COC must be as well.
"p'" = the far focal point of the secondary (the front point)
"f" = EFL of primary mirror
"R" = Radius of Curvature of the secondary mirror
"b" = distance from primary vertex to Cass focus
"A" = secondary amplification
"SCC" = Conic Constant (how hyperbolic it is) for the secondary.
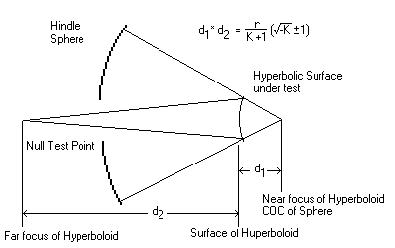 The Ronchi or Foucault tester is located at the Cassegrain focus, which is the other focal point for the secondary. Light from the tester proceeds to the secondary, then to the Hindle sphere, where it reverses direction exactly, then back to the secondary, then back to Cass focus.
The airspace between the Hindle sphere and the secondary vertex is the Hindle ROC minus the "p" (rear focus point of the secondary) distance.
Now that we have all of the various numbers of the scope all figured out, the test is really pretty easy to setup (in theory anyway) and perform.
First thing that we need is all of the hardware to hold all of the optics and testers.
This means that we need:
The Ronchi or Foucault tester is located at the Cassegrain focus, which is the other focal point for the secondary. Light from the tester proceeds to the secondary, then to the Hindle sphere, where it reverses direction exactly, then back to the secondary, then back to Cass focus.
The airspace between the Hindle sphere and the secondary vertex is the Hindle ROC minus the "p" (rear focus point of the secondary) distance.
Now that we have all of the various numbers of the scope all figured out, the test is really pretty easy to setup (in theory anyway) and perform.
First thing that we need is all of the hardware to hold all of the optics and testers.
This means that we need:
Hindle sphere holder that can move the ROC up and down and left and right.
An aiming device that will help aim the sphere to the right place - the Foucault tester can provide the necessary aiming capabilities.
It would also make things easier if the testing apparatus (Foucault Tester?) is attached to the back if the focal point is nicely close enough.
This will make that much of the system easier to handle.
You then need a holder for the secondary and that also needs to be able to tilt and rotate left and right.
The secondary holder should also have a good set of mountings so that you can have some kind of reputability (mark a top on the secondary) when you're testing it.
Remember that you're going to be taking the secondary off, doing a couple of licks with the lap and then putting it back on the tester and being able to only move the secondary just a little bit will be a big help.
You should also have the secondary holder on a set of rails of some kind so that you can make short in and out movements. These can be a bit cruder than those of the other motions - the rails mostly will be just guiding the holder so that it doesn't get way out of the proper angle.
You will also need a good measuring stick to measure the distance from the Hindle sphere to the surface of the secondary. This measurement is very critical as it sets what the actual shape of the glass is going to be and we don't want any Hubble Telescope Mirrors made here if we can help it.
If you're ready to start testing, put the Hindle sphere (you already know exactly what it's radius is) up on it's mount, place the secondary so that the distance to it is the ROC of the Hindle sphere minus the (virtual) near focus of the secondary is at the same place.
After the Hindle Sphere and Secondary is setup, the Foucault tester (where you are going to actually test the secondary) goes at the position that is the far focus point of the secondary (marked as p' in the formulas above) from the surface of the secondary.
Get everything lined up so that you can see the Hindle sphere centered in the secondary thus making everything coaxial and test. Everything should be at the same height and when looking at the image coming back from the optics at the knifeedge, it too should be at the correct height.
As a last check, make sure that all of your measurements are correct and the Foucault tester should be exactly where you think that it should be.
If the Focuault tester isn't giving a nice spherical looking null, but rather it's inside or outside of Focus, you've probably measured something wrong or you just have the wrong shape to the Secondary and the latter is probably true.
Three months later, I've come back and looked at this page and i don't know where I got the formula in the Hindle Test drawing. At the moment, it makes no real sense to me. At this point, I'm not going to remove it but it's all a mystery to me.
One of the things that I do know is that there is a slight problem in raytracing the test and, while I figure that the problem is actually the raytracer, there is always the possibility that there needs to be some little modification to the distance of the secondary from the Hindle sphere.
I ran the raytracing with a Hindle Sphere of 300mm diameter and a secondary with a first focus of 25mm and a second focus of -176mm. The distance from the Hindle should have been 175mm but in the raytracer, the actual distance is about 275.03891 but the distance keeps changing depending upon the number of rays that I trace. From this I am assuming that there is a slight problem with the raytracer as the number of rays should not change the best focus (which isn't as good as it should be) at all. When running with longer distances, the problem tends to go away and that tends to indicate to me that the formula distances for the test are indeed correct and that the raytracer is wrong.
 The first thing to do is to figure out what you are doing as related to how big the convex surface is that you are going to test and it's various focii.
What I am interested in here is the testing for a hyperbolic surface for the Cassegrain telescope.
The secondary of a Cassegrain telescope is usually a hyperbolic surface of some pair of focii.
The near focus is behind the surface (on the concave side) and the far focus is on the front side of the surface.
You need to know both of these focii in order to be able to test the surface.
The first thing to do is to figure out what you are doing as related to how big the convex surface is that you are going to test and it's various focii.
What I am interested in here is the testing for a hyperbolic surface for the Cassegrain telescope.
The secondary of a Cassegrain telescope is usually a hyperbolic surface of some pair of focii.
The near focus is behind the surface (on the concave side) and the far focus is on the front side of the surface.
You need to know both of these focii in order to be able to test the surface. The Ronchi or Foucault tester is located at the Cassegrain focus, which is the other focal point for the secondary. Light from the tester proceeds to the secondary, then to the Hindle sphere, where it reverses direction exactly, then back to the secondary, then back to Cass focus.
The airspace between the Hindle sphere and the secondary vertex is the Hindle ROC minus the "p" (rear focus point of the secondary) distance.
Now that we have all of the various numbers of the scope all figured out, the test is really pretty easy to setup (in theory anyway) and perform.
First thing that we need is all of the hardware to hold all of the optics and testers.
This means that we need:
The Ronchi or Foucault tester is located at the Cassegrain focus, which is the other focal point for the secondary. Light from the tester proceeds to the secondary, then to the Hindle sphere, where it reverses direction exactly, then back to the secondary, then back to Cass focus.
The airspace between the Hindle sphere and the secondary vertex is the Hindle ROC minus the "p" (rear focus point of the secondary) distance.
Now that we have all of the various numbers of the scope all figured out, the test is really pretty easy to setup (in theory anyway) and perform.
First thing that we need is all of the hardware to hold all of the optics and testers.
This means that we need: