Understanding Foucault:
A Primer for Beginners

Introduction

      A delightful experience with rare flavor awaits one who beholds a celestial wonder with a mirror crafted with his or her hands. Most persons making their first telescope mirror also find another kind of rare flavor in the experience: the reward of meeting a challenge that requires discipline and concentration of one's mental faculties.

      Almost certainly the last phase of mirror making, where one imparts the final, precisely defined curve to the mirror's reflective surface, is the most challenging. This final stage of mirror making is known as figuring, inasmuch as it is a process of altering the mirror's curve, or figure into the one required for proper function, usually into that of a parabola for the Newtonian type of telescope. The process of figuring is essentially a process of selectively removing very minute amounts of glass in the proper places to bring the curve to the required form of the parabola. In order to guide the process of figuring we need a sensitive test that will accurately show us the mirror's true figure at every stage of the work.

      With this treatise, I will show that for the amateur Foucault test has altogether more advantages and fewer disadvantages than any other method of testing. The method is extremely versatile and more than adequately precise. The Foucault test is even adequate enough for the production of a fine primary mirror for the classical Cassegrain reflector. I have written these pages in a new way in order to make the basic foundation concepts understandable in as intuitive a way as possible, not assuming any previous familiarity on the part of the reader with any of these founding concepts.

      For this reason it seems appropriate to insert a necessary note for those experienced and knowledgeable persons who may want to offer comment on these pages. You will find many illustrations, descriptions, and explanations that will strike you as perhaps incomplete, or not quite precisely literal, or not exhaustive on the subject. I ask all of you to bear in mind that I am trying to educate the beginner, rather than confuse him or her with too much unnecessary information. My goal is to teach first principles first.

Testing in General, Briefly

      Monitoring the developing figure of a mirror can be done with a wide variety of methods. All of these methods fall under two basic genera with their several different species: tests done at center of curvature, and tests done at focus. We consider testing at conjugate foci as a variation of testing at center of curvature.

      Testing at focus is very convenient and is the preferred method for many advanced amateurs. The commercial houses also usually prefer it. For the amateur with limited resources wanting to make only one, or a few mirrors, it is not so suitable as testing at center of curvature. This is because both of the best forms of testing at focus, null testing and interferometry, require auxiliary optics that are either prohibitively expensive, or overly challenging for the beginner to fabricate. Thus, we will conclude that testing at focus is not convenient for the purposes of beginners.

      That leaves us with the other genus of testing with its various species: tests done at center of curvature. The best forms of this type of testing fall (at least approximately, if not precisely) under two basic forms: null tests, and non-null, quantitative tests.

      Null testing at center of curvature we dismiss as not convenient for the purposes of the beginner for the same reason we dismissed it as a testing method for use at focus: it requires auxiliary optics either expensive or difficult to fabricate. In addition, this form of testing introduces an extra level of opportunity for error - I will merely cite the tragic case of the Hubble telescope's seriously flawed optics for an example of null testing at center of curvature gone seriously awry, even in the hands of seasoned experts.

      At last we come to that other species of tests at center of curvature: non-null, quantitative tests. There are two best, most useful sub-species of this kind of testing: the Gaviola, or so-called "Caustic" test, and lastly, the Foucault test.

      A very "great light" in the optical industry once dismissed, in conversation with me, both Caustic (and Foucault) as "useless". After finally mastering both these forms of testing, I understood why he'd made this remark: he used interferometry, a far less cognitively challenging method for testing, and did not have an adequate conceptual understanding of the other methods.

      Caustic is capable of monitoring the developing curve on a mirror being figured to an extremely high degree of accuracy. This very precise, rigorous form of testing is, however, both time consuming and tedious in its execution. Additionally, the test apparatus is expensive to purchase, or overly challenging for one without machine tools or machining skills to fabricate. So we will pass on Caustic as also not suitable for the beginner's purposes.

      We finally come, then, to Foucault. In defense of its merits as weighed against its demerits, I refer the reader again to my general comments in the second paragraph of my introduction. Additionally, I would like to say in praise of Foucault that it is peculiarly "idiot proof" in a way that null testing at center of curvature is not. Again, I cite the near disaster of the Hubble telescope as an example of the kind of error that can happen with null testing at center of curvature. This kind of error can't happen with the Foucault test; the nature of the test set-up for the Foucault test prevents it from "telling a lie". Lastly, I want to add that neither machine tools nor machinist's skills are required to construct a very adequate test apparatus for the Foucault test. Time has tested Foucault- "Nothing tests truth like time". (I will cover testers and their design and construction after teaching testing essentials- building a tester is easy).

First Essential Foundation Lesson:

      Now this method of molding a mirror helps us understand some things. Firstly, it helps make clear what is meant when we say that this mirror's curve is spherical; of course it is spherical- words are not really needed to describe its curve- its shape is a direct impression of the big sphere of Krell (Krell being a particular material known only to the Krell civilization of which we don't really need to know more of) metal. So we have a spherical mirror now, which after further work will become a telescope mirror. Let's look at some features of this spherical mirror. We understand now that it has a spherical shape, or figure, after having being molded with the big sphere of Krell metal. We will often have occasion to refer to its figure's radius of curvature. Please look at figure 1 again; it is immediately apparent from figure 1 what we mean by radius of curvature when referring to this mirror's spherical figure; its radius of curvature is identical to the radius of curvature of the surface of the big ball of Krell metal used to mold it with. So our imaginary molding technique for impressing the initial concave curve onto our mirror has taught us two things- what is meant by the term spherical, as a description of a mirror's figure, and what is meant when we speak of its radius of curvature.

Next Essential Foundation Lesson

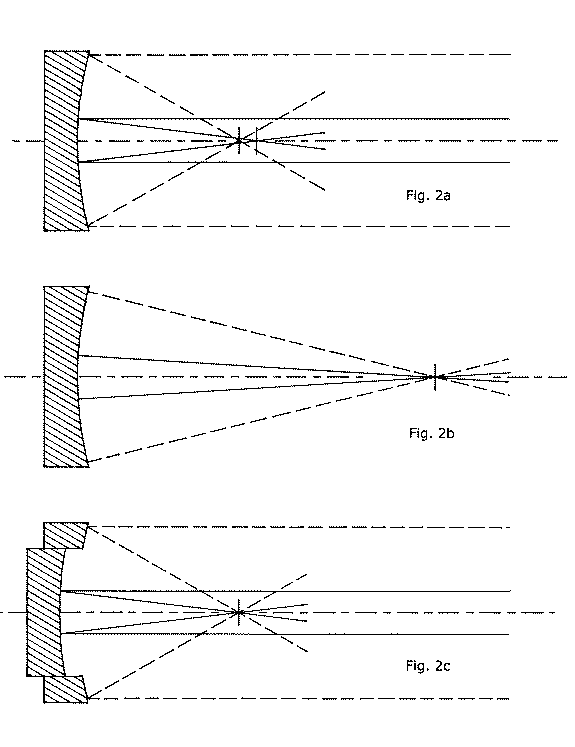
      While learning this next lesson, we will be referring to figure 2(a) and figure 2(b). Figure 2(a) shows a view of our newly molded mirror with its concave, spherical figure in cross section, receiving four parallel rays of light as they enter from the right side of the diagram. These rays of light are parallel because they originate from a very small source of light a very great distance away from our mirror- we will specify that the light source is infinitely far away. The rays of light striking the areas of the mirror's surface near its edge are shown as dashed; the rays of light striking the mirror's surface near its central regions are shown as unbroken. The line shown proceeding through the center of the face of the mirror we shall call its optical axis. Strictly speaking, a spherical mirror does not have an optical axis, but we will pretend that it does, for teaching purposes.

      Now, looking at figure 2(a), we can see that the light rays are reflected from the concave spherical surface of our mirror and focused onto a specific region along the mirror's optical axis. A casual glance suggests that the mirror will focus all four light rays down onto the same point lying on the optical axis, but a close inspection will reveal that this is not quite the case. The rays of light that were reflected from the outside regions of the mirror's concave spherical surface (represented by the dashed lines) come to a focus at a point lying on its optical axis slightly closer to the mirror than those rays of light reflected from the interior regions of the mirror's concave spherical surface. In our illustration, two short, vertical lines mark these two different locations along the optical axis. We will think of these two short, vertical lines as representing two different locations of a small square of ground glass, on which to see the focused image of the infinitely distant light source. Or, just as usefully, we might think of them as representing two different locations of a small square of photographic film, with which to record the focused image of the infinitely distant light source. What is essential for us to understand here is that a mirror with a spherical figure (we will call this kind of mirror a "spherical mirror") receiving light from infinity cannot focus all of this light reflected from its inner and outer zones into the same focal plane. This defect is known as spherical aberration (naturally enough).

      The mirror in our example as molded by the Krell in their optical plant has a very short focal length; really, its focal length is even too short for us to use it in a telescope. We have made it very short so that the diagrams will be clearer and more instructive. When we speak of a mirror's focal length, we mean, of course, the distance from the mirror's concave, reflective front surface to the point (or, more precisely, a field of all possible points, a "focal plane") into which any given bundle of parallel rays received by the mirror from infinity will be focused. In short, the focal length is the distance from the front surface of the mirror to its image, or focal plane. The diameter of a mirror, divided into its focal length, gives us its focal ratio. We will pretend that our Krell opticians have molded us a 12" mirror with only a 12" focal length. Thus, the focal ratio of our mirror is unity, and expressed (by convention) as f/1.

      While we are still considering figure 2(a) it will be helpful, here, to understand that this illustration can be thought of as representing only how a mirror makes an image of a very distant, apparently very small, single light source, such as a single star that the telescope is aimed directly at. A little thought will make it apparent, however, that for an image field comprised of more than a single star, such as for instance a galaxy, a mirror will be receiving many different bundles of parallel light from many different points of origin in its field of view, each of these bundles approaching the mirror at a slightly different angle, with each bundle reflected at a correspondingly slightly different angle from the mirror and focused into separate, disparate points in the focal plane, building up an image all across this plane.

We Need a Mirror

      In order to begin learning the Foucault test, we need a concave mirror. I cover the mechanics of grinding and polishing the preliminary curve onto the glass in another paper- we are interested here in learning testing so that we can figure the final, correct curve onto the glass to enable it to give sharp images.

      We're going to make our mirror in an imaginary way in order to teach you your very first essential foundation lesson for understanding the Foucault test.

      Perhaps some civilization beyond the earth, with an advanced technology, makes mirrors by a method we shall theorize. Maybe the vanished "Krell" civilization on Altair 4 made their mirrors in the way we shall describe. The Krell opticians will demonstrate how they will impress the initial concave curve onto a twelve inch mirror with a very short focal length. For our first lessons in our treatise on Foucault testing, a very short focal length mirror serves for clarity in the illustrations better than a longer focal length mirror. We will pretend that the Foucault test will serve well for testing such a very short focal length mirror- even though we know that the Foucault test is not satisfactory for testing mirrors of extremely short focal length. Remember that our purpose is to teach.

Molding a Mirror

      Perhaps archaeologists will discover that the long vanished Krell opticians did not grind their mirrors, but molded them. Let us theorize that they used a large, perfectly spherical ball of their fabulously durable "Krell metal" to impress the initial concave curve onto a mirror being made. We will refer to figure 1 as we discuss this molding technique. Looking at figure 1, we see a depiction of a large sphere, drawn as if it were transparent. A dotted line of longitude, and a similar line of latitude, are drawn onto the surface of the sphere to help convey its three dimensional shape. On the far side of this apparently transparent sphere of Krell metal we can see a telescope mirror pressed up against its smooth, spherical surface.

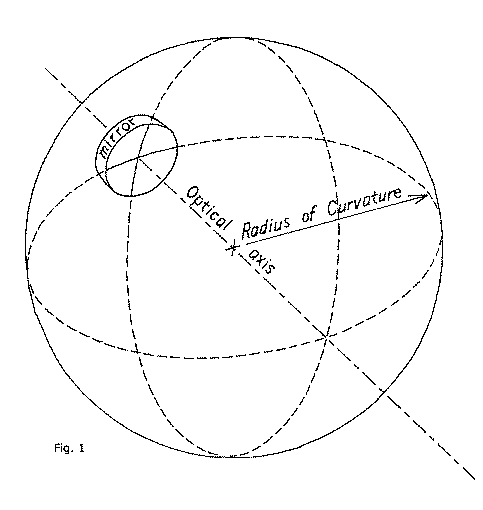
      And this is the first step in Krell mirror making: the initial curve is impressed onto the surface of the glass after it is heated to near melting by pressing the mold with the hot glass up against the surface of the big sphere. One can plainly see that the shape of the curve impressed onto the glass with this molding procedure is an exact representation of the shape of that section of the sphere's surface that it was held in contact with.