Next Lessons
We will not call this next instruction an "essential foundation lesson", but it will help prepare you for one.
We've seen that a spherical mirror cannot focus light from infinity that has been reflected from different areas of its surface all into one focal plane. This defect is known as spherical aberration and will prevent the mirror from focusing light accurately enough to form a sharp image.
Fixing the Defect
How can we possibly remedy this defect, this inability of a spherical mirror to accurately focus all its reflected light into one focal plane? If we look again at figure 2(a) we can find a clue as to one possible remedy- since the rays of light that are being focused by the near-central regions of the mirror are coming to a focus farther away from the mirror, why can't we just move the central portion of the mirror back a ways, until its focal plane is congruent (in the same location) as the focal plane for light focused from the outer (near mirror's edge) regions? Figure 2(c) shows how this remedy might work: note how the central portion of the mirror has been parted from an outer annulus, and moved backwards by a distance required to bring its focal plane congruent with that for the outer annulus. The remedy was actually tried by a famous nineteenth century telescope builder, Lord Rosse, whose chief contribution to astronomy was his giant reflector at Birr castle and his discoveries with it. The remedy is impractical for several reasons, however, and probably tried only once. But I have shown you Lord Rosse's experiment for instructional reasons- we are going to use his curious, once ever two-component mirror to learn an interesting lesson that will help us understand the Foucault test. Before we meet our "Lord Rosse Special" again, however, we need to learn about the knife-edge.
Leon Foucault
The nineteenth century saw many important foundation developments that contributed to the perfection of the modern reflecting telescope. Leon Foucault (1819-1868) contributed some of the most important of these innovations. In addition to demonstrating the superiority of glass (with silver coating) over speculum metal for mirrors, he presented the world with a powerful method for critically surveying optical surfaces- the knife-edge test. In his hands and the hands of his followers various developments and applications of the use of the knife-edge as an adjunct for accurately figuring optical surfaces were developed over time.
The Knife Edge
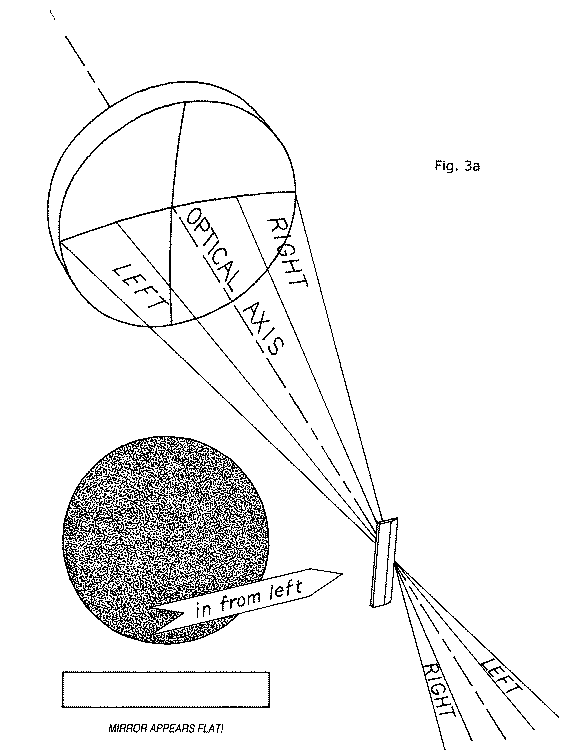
Let's look now at figure 3a. We have our 12" spherical mirror, molded for us by the Krell opticians, standing on edge. We've left the two meridians of longitude and latitude, impressed onto the mirror's front surface from the big ball of Krell metal, to remind us of the mirror's concave shape.

Four rays of light are depicted as being focused by our mirror down to a point, apparently just adjacent the edge of a small razor blade standing on its end. Please note that the edge of the blade is extremely close to the mirror's optical axis. These light rays have emanated from a very tiny light source located on our mirror's optical axis at the center of its radius of curvature and fanned out to its concave surface, to be reflected back along their outgoing paths to converge right back onto their tiny light source.
After converging onto their original source, they continue on, fanning out and away. Although we show only four light rays fanning out from this tiny bulb, in order to keep the diagram uncluttered, we will keep in mind that in reality there are light rays fanning out from this little light source in great numbers in every direction and are striking the mirror's front surface all over.
In this illustration our tiny light bulb at center of curvature and the razor blade's edge are virtually in the same location. In order to keep the illustrations as uncluttered as possible, we will adopt the convention of not showing this light source at center of curvature.
The mirror is actually forming an image of our tiny light source right at center of curvature, and even if we do not have a piece of ground glass or film in place here for the image to be focused on, it will still be in place here, just suspended in the air - a so-called "aerial image".
Now we are going to do an experiment. First, we will move the razor blade away from the optical axis to the left, slightly - just enough so that we are sure it is not obstructing any of the reflected rays of light crossing over the optical axis here at center of curvature (we will shorten "center of curvature" to "C of C" from here on out). Next, one of us places his or her eye in position on the mirror's optical axis just behind and very close to the tiny aerial image formed there at C of C. Now, with one's eye placed very close to this tiny image, one's eye will not be able to focus on it and see it, but rather, one will see the mirror beyond it. The mirror will appear brightly and evenly illuminated all over, because it is reflecting the light from the tiny light source equally from every portion of its surface.
Next, we begin to bring the razor blade in from the left, very slowly, until its edge begins to obstruct, or occult part of this light returning from the mirror. Now, inasmuch as each and every part of the tiny image of the light bulb is receiving a bundle of light originating from the mirror's entire surface, when the razor blade begins to obstruct it, the light in each of these bundles from the mirror is reduced equally and simultaneously from every part of the mirror's surface, and the mirror begins to darken all over simultaneously and equally, "graying out" all over, uniformly. We may halt the advance of the knife-edge (KE) when it is obstructing about half of the returning light from the mirror; or, we may continue its advance until the returning light is entirely cut off. If our mirror is accurately spherical, and the KE approaches and crosses the optical axis at exactly the C of C, the mirror will darken, or null, simultaneously, all over its surface. When we use the KE to examine our spherical mirror from the vantage point of its C of C this way, the mirror will appear perfectly flat. We know for certain that it is spherically concave, but nevertheless it appears flat when viewed this way. And as it turns out, there are important advantages for us in pretending, or imagining the mirror as flat, instead of concave. And this is the essence of another essential foundation lesson: we will adopt the convention of always visualizing the mirror's surface as flat, and any deviations from this imaginary flat figure will always be visualized and depicted as such.
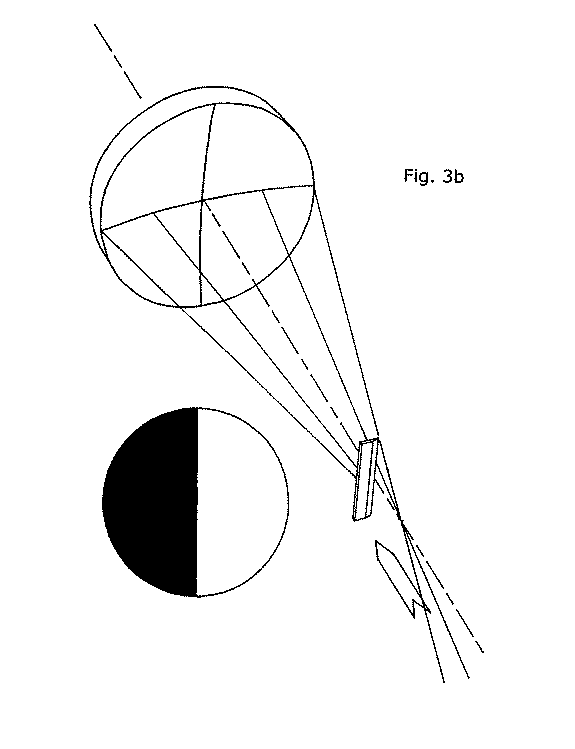
Now, let us consider figure 3b. Our razor blade (KE) can be moved at right angles to the mirror's optical axis, and also parallel to its optical axis, toward or away from the mirror. In figure 3(b) we have moved it a little ways toward the mirror, leaving its edge just adjacent the optical axis. The KE is now blocking only those rays of light coming from the left side of the mirror, and only its left side appears dark. If we withdraw the KE to the left, away from the optical axis, this dark shadow on the left side of the mirror will recede to the left, also. If we advance the KE back in again to the optical axis, the shadow will reappear and advance in the same direction across the mirror's surface. If we continue advancing the KE all the way across the optical axis (OA) until all of the returning rays of light are blocked, the entire mirror will go dark as the KE's shadow advances all the way across the mirror from left to right.
Now, let's back the KE away from the mirror along its OA, passing through C of C until we are beyond it by about the same distance as we were just previously inside it (closer to the mirror than C of C) as shown in figure 3(c).
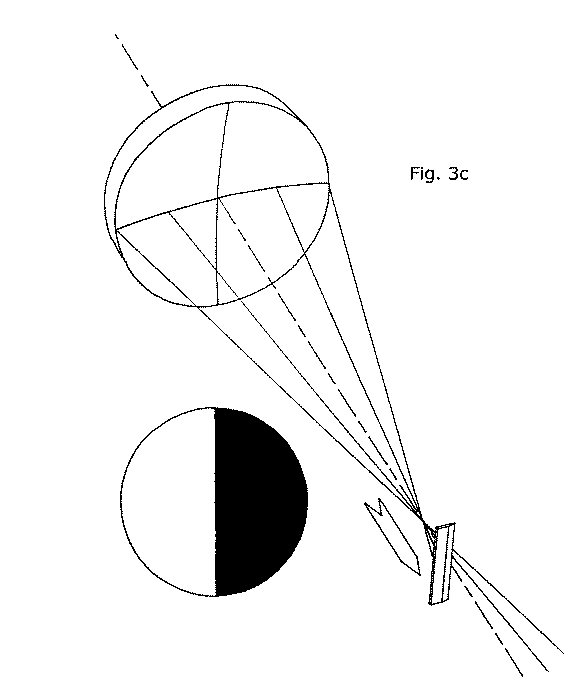
Suddenly, even though we have not moved the KE laterally, the right half of the mirror now appears darkened! Look at the illustration carefully: with the KE beyond C of C, it is now blocking the rays of light from the right half of the mirror after they've crossed the OA. The light rays from the left half of the mirror, however, have crossed over the OA in the other direction, away from the KE, and are not obstructed by it at all. Now, if we back the KE out to the left again, away from the optical axis, the shadow on the right side of the mirror will advance in the opposite direction of the KE, towards the right. If we back the KE out all the way to the left, so that it no longer obstructs any of the returning rays from the right half of the mirror, the mirror will again appear bright all over. Alternatively, if we advance the KE back in again from the left until all of the rays of light returning from the mirror are obstructed (occulted) then the mirror will go dark all over as the KE's shadow advances in from the right, again moving in the opposite direction as the KE.
We've just made a wonderful discovery, and learned our next, essential foundation lesson: the KE can tell us whether we are inside of, outside of, or exactly at the center of curvature of a spherical mirror.
The "Lord Rosse Special"
We've learned that the knife-edge can tell us just about one important thing about a perfectly spherical mirror - where its center of curvature is. And although spherical concave mirrors have their places in astronomical optics, we are primarily going to concern ourselves with another species of concave curve that is not as simple as the sphere. Remember - a spherical mirror suffers from spherical aberration- a characteristic that prevents it from accurately focusing light from infinity, preventing it from forming sharp images.
Remember our discussion about Lord Rosse's efforts to cure spherical aberration with his curious two-component mirror? We're going to use his novel mirror to learn a new, essential foundation lesson.
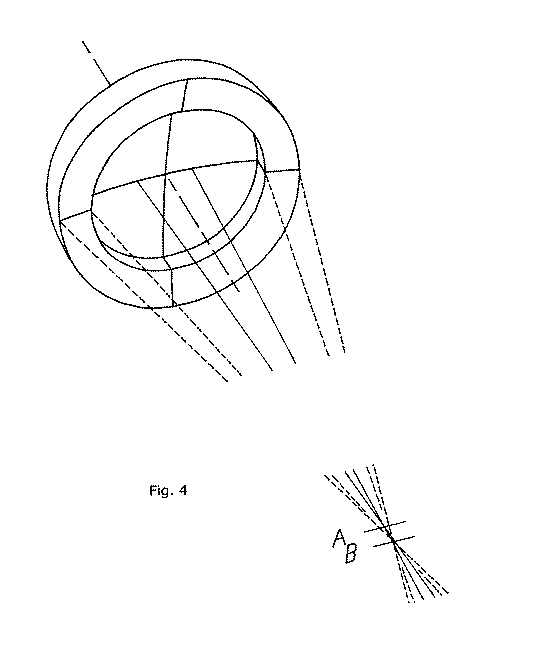
Let's take a look at figure 4. It shows us Lord Rosse's two-component mirror standing on edge. We've put two meridians across its front surface to help us visualize its shape. This mirror was made by parting a single, one piece spherical mirror into two components. Before it was parted and the two components relocated slightly with respect to each other, it had, of course, a single radius of curvature and therefore a single center of curvature. But now this "compound" mirror has two different centers of curvature. They are marked in the diagram as two short lines lying across the optical axis in slightly different locations, at "A" and "B". Two unbroken lines representing two rays of light are shown emanating from the C of C marked "A" and fanning out, striking the interior of the central component of the mirror. After being reflected from this area, they converge back on their C of C, crossing the OA at that location and then fanning out beyond. Four dashed lines, rays of light, are similarly shown fanning out and striking the outside component or annulus of the mirror and then being reflected back to their C of C, crossing the optical axis there and fanning out beyond. Let's take a close-up look at this region of the OA where all of these rays are crossing it.
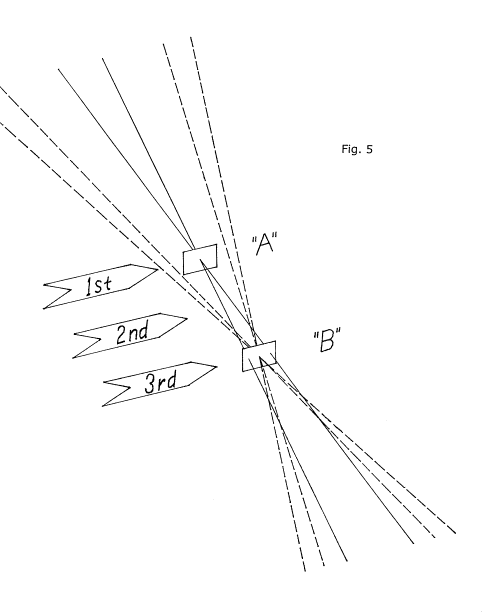
In figure 5 we've zoomed in close to see what's happening more clearly where these light rays are crossing the OA. At each center of curvature for each component of the mirror we've positioned a little square of ground glass (or we may think of it as a little square of film) to represent each component's center of curvature. We have located three "arrows", labeled 1st, 2nd, and 3rd for three positions along the optical axis. We're going to explore the optical axis in this region with the KE, and inspect the mirror with it positioned, in turn, from each of these locations represented by the little arrows. We show these locations identified by arrows to remind us that in each location we will bring the KE in from the left, starting with it well clear of any returning light rays from the mirror, so that we may observe the order of progression of the unfolding appearances as the KE is moved inwards. We will omit any depiction of our "imaginary" light source at each center of curvature to keep the drawing uncluttered. And this time we will not show the knife edge, either, leaving you to imagine it and its action as it moves inwards from each of these locations in turn.
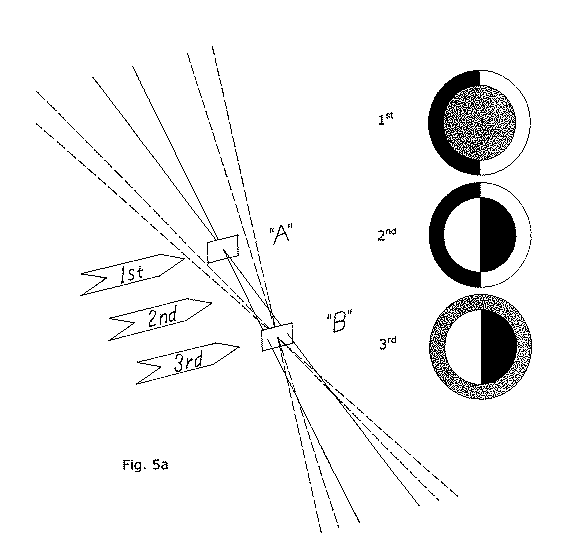
Let's start with the KE in the position marked 1st, the position closest to the mirror, and work successively outwards to the other locations, in turn.
As we begin moving the KE in from the left, it first encounters light rays returning from the left half of the outside annulus of the mirror, obstructing its left-most rays first. As the KE continues slowly advancing inwards, more and more light from the annulus is obstructed, progressively from left to right, and we see a very dark shadow proceeding inwards across the annulus from left to right. The shadow, so far, is moving in the same direction as the KE. By the time the KE is nearly just adjacent the optical axis, the left half of the mirror's outside annulus is almost completely filled in with dark shadow. Finally, as the KE moves the very last, tiny increment of distance to bring its edge just to the OA, it begins to partially and simultaneously obstruct light from every part of the central component of the mirror here where it crosses the optical axis. As the KE obstructs this light, the central component grays out, or "nulls". We have detected the central component's center of curvature with the KE. Halting the KE's advance now, we note the mirror's overall appearance, and it appears as in fig. 5(a), with the left half of the outside annulus completely dark, its returning light completely obstructed by the KE. The central region is nulled, with its light only about fifty percent obstructed. The right half of the outer annulus is still completely bright, as all of its rays pass well clear of the KE's edge, not at all obstructed in the least.
After taking careful note of the mirror's appearance with the KE in its last position at the arrow marked 1st, we next withdraw it laterally, away from the OA until no light from the mirror is obstructed, and then back it away from the mirror until it is at the arrow marked 2nd, midway between the centers of curvature of both the mirror's components. With one's eye again in place on the optical axis looking at the mirror, the KE is again brought very slowly in from the left until it begins to obstruct the leftmost rays of light returning from the mirror. As in the 1st position, the leftmost regions of the outside annulus begin to darken first as we see the KE's shadow again move in from the left, in the same direction as the motion of the advancing KE. Continuing the slow, rightward motion of the KE, we begin to get close to the OA and the left-hand side of the outside annulus becomes nearly filled with dark shadow as before when we were working at the 1st position closer to the mirror. But then, a curious thing begins to happen: as the KE continues its slow advance up to the OA a dark shadow begins to move in from the right, traveling leftwards across the right half of the central component of the mirror. The rightmost regions of this component begin to darken as the KE obstructs their reflected light on the left side of the OA where they've crossed over a little ways after having passed through C of C for this central component of the mirror. Continuing the KE's advance right up to the edge of the OA we observe this shadow continue and complete its advance inwards from the right hand side of the central component until the entire right half of this component is in dark shadow. After stopping the KE's advance right at the OA, we note the overall appearance of the mirror. The light from the left half of the outside annulus is completely blocked, and the light from the right half of the inside component is completely blocked, and both of these areas appear very dark. However, the returning light from the right half of the outside annulus passes well clear of the KE and it remains brightly illuminated. In addition, the light from the left half of the inside component passes well clear of the KE and this area also remains fully illuminated. The overall appearance of the mirror is as in fig. 5a, "2nd".
We will finally relocate the KE in the 3rd position, starting again with it well clear of all returning light rays and then advancing it in towards the OA from the left. As it advances in from the left, the first light it encounters and obstructs is that returning from the right half of the inside component of the mirror. This light has already crossed over the OA and is well clear of it to the left in this 3rd position. As the KE continues its inward advance towards the OA, the edge of the dark shadow advancing in across the right half of the central component moves leftwards, in the opposite direction of the KE's motion until the right half of the inside component is nearly all dark. Then, as the KE advances the last small increment of distance up to the OA, it begins to obstruct the returning light rays from every portion of the outside annulus' surface equally and simultaneously, causing this central area to gray out, or null all over simultaneously. The KE has detected the C of C for this outside annulus of the mirror. We halt the KE's advance here, right at the optical axis, and survey the mirror, noting its appearance, as in fig. 5(a), "3rd". The right half of the inside component is completely dark, all its returning light occulted, and the left half is completely bright, none of its returning light occulted. The outside annulus is evenly nulled, as our KE is precisely at its center of curvature.
Exploring the optical axis of our "Lord Rosse Special" with the knife-edge has been our first experience in surveying the surface of a concave mirror whose figure is something other than a simple sphere. We've garnered many different lessons with this exercise that will now be well understood intuitively, without further necessity to elaborate verbally. One, however, needs to be gotten in mind in a very unequivocal fashion, and so we now state it here as an essential foundation lesson: The appearance of any concave mirror when surveyed with the knife edge will always be different when viewed from different locations for the knife edge along the optical axis.
Correcting Spherical Aberration
Before leaving our "Lord Rosse Special" it will be instructive to understand why it didn't work so well as a remedy for spherical aberration.
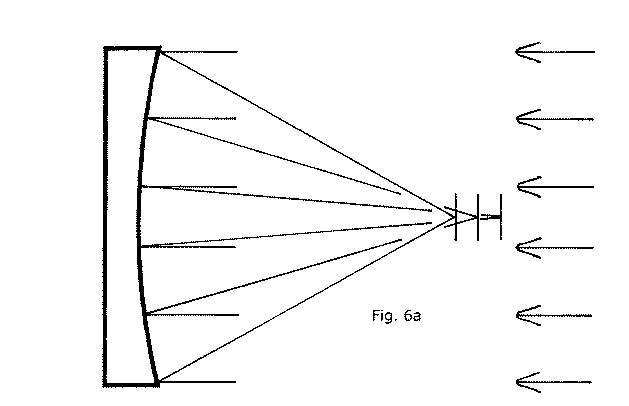
In figure 6(a) we show a very short focus mirror in cross section receiving light rays from infinity and focusing them along a short region of its OA, as in our earlier diagram, fig. 2(a). In that previous diagram we showed light rays from infinity striking the mirror near its edge and near its center and being reflected onto a short region of the OA. For fig. 6(a), however, we show some rays in addition to those for the central and near edge regions. These rays are striking the mirror's face in a zone intermediate between its edge and center regions. The illustration makes it plain that the spherical mirror cannot focus rays of light reflected from any of these zones into the same focal plane. Three short lines lying across the OA represent the three different focal planes for light reflected from these three zones or areas of the mirror.
Contemplating this diagram should lead one to an intuitive insight: for as many zones as we care to demarcate the mirror's concave surface into there will be as many disparate focal planes for. It should now be clear why a two component "Lord Rosse Special" will not work well; it is optimized for only two zones for the entire mirror: a narrow zone near the edge, and a small region very near the center. All other zones for either component of the two component special will still have widely disparate focal planes.
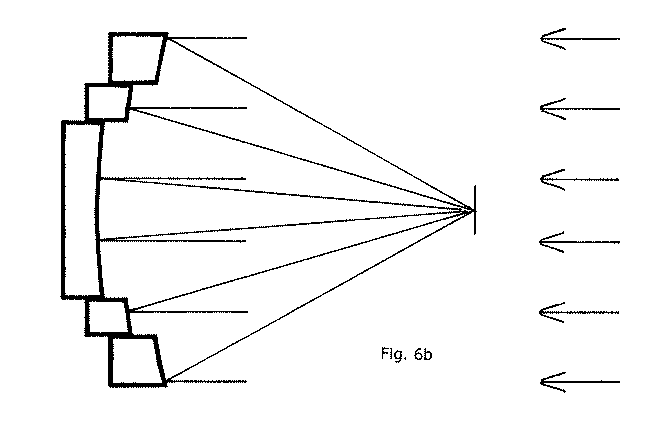
Fig. 6(b) shows a hypothetical three component mirror in cross section. We might reasonably expect this three component mirror to work better than a two component one, focusing reflected light from the zone intermediate between its edge and center into a focal plane more congruent with those for focused light from the other zones. But a little thought here will reveal the impossibility of such an approach: each of the three new components is still a section of a sphere, and therefore will each have disparate focal planes for its different zones. In order to optimize the correction to bring the many disparate focal planes congruent, we would have to go on "surgically" subdividing the mirror further and further into more and more nested components, annuli, offsetting each one by the required amount from its neighbor along the OA. However, this exercise becomes more silly as you divide even more as it's basically impossible to actually do this in reality.
As a conceptual exercise, however, Lord Rosse's approach points the way to a more practical solution: we can offset the successively more central regions of the mirror, successively, from the successively nearer edge regions (relative to a sphere) simply by excavating these successively nearer central regions more deeply. We will then no longer have a concave surface representing a revolution of a circle (a sphere) but some other species of figure of revolution. And this is in essence the time-tested method for altering a spherical mirror's figure into one for which all zones of its concave surface have congruent focal planes, i.e., one that will focus light from its entire surface into the same focal plane. The particular species of surface of revolution that can do this is a curve that geometers long ago designated as one of a family of specifically defined sections of a cone: the paraboloid which has a gradually increasing COC as the distance from the center is increased - each step in the exercise above having a slightly larger ROC. And now we are well enough prepared with previously learned founding concepts to introduce the next very important essential foundation lesson: the properties of the sphere and the paraboloid are exactly reversed with respect to each other with regards to each's conjugate focal planes. The sphere, while unable to focus light from infinity into one focal plane, will exactly focus all light received from its center of radius of curvature into one focal plane. Alternatively, the paraboloid, while unable to focus all light from its center of curvature into one focal plane, will exactly focus all light received from infinity into one focal plane. Strictly speaking, a paraboloid does not have a center of radius of curvature, since it is not a sphere; but we will take liberty and use language loosely here in order to help illustrate a concept.
This curious order of features of the curves of conic sections seems almost to have been by design for those of us who want a convenient and quantitatively precise test procedure for monitoring the development of the paraboloid during figuring. In particular, we are happy that the paraboloid cannot return light from a source located at its approximate center of curvature into one focal plane, but instead returns it into different focal planes strung out along its optical axis.
Summary, in Graphic
We're ready to learn the actual test procedure now. Since the essence of the test is embodied in our last essential foundation lesson, we will briefly recap this lesson in a compact, graphical form, so that you will get it firmly in mind. Let's look at figure 7.
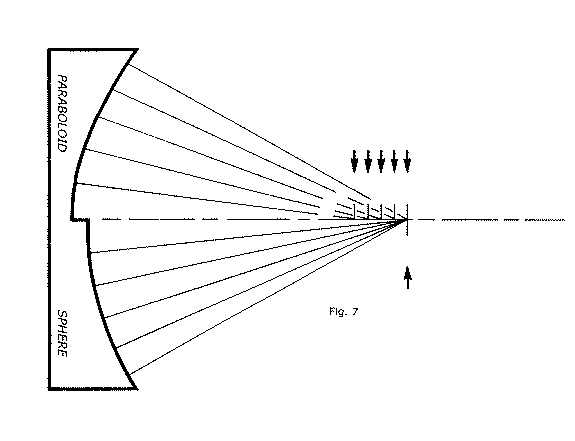
We show yet another, curious, hypothetical mirror in cross section here. This imaginary mirror is divided into two different regions: the bottom half has been left spherical, but the top half has been figured paraboloidal. On the optical axis (out to the right) we've located the center of curvature of the lower, spherical half of the mirror. Light rays are fanning out from this C of C, striking the mirror, and returning back to its C of C. The little arrow below the optical axis marks the C of C.
Now, the upper half of this mirror is paraboloidal. We may reference it with the lower, spherical half of the mirror by specifying that it's very edge zone or region is congruent with the sphere represented by its lower half. This illustration makes clear, at a glance, what we used words to describe as our last essential foundation lesson: the sphere can return all light originating at its C of C precisely back to that C of C; the paraboloid cannot. For this paraboloidal part of the mirror, we show light rays emanating from the C of C of the lower, spherical part its edge is congruent with. Note that it can return only light from this edge zone back to the sphere's C of C. All regions, zone wise successively closer to the center of this paraboloid, will return light to focal planes that are successively closer to the mirror. The five different arrows pointing downwards indicate the five different focal planes for light reflected from the five different zones on the paraboloid (the same zones, radius wise, as for the sphere). All that remains is to show you that the disparity between these various focal planes for the paraboloid can be specified for the figure we desire, and that they can be commanded into their desired locations along the OA by figuring the mirror.
Now, although not critically necessary, it will be useful to understand an interesting lesson here before we begin testing.
In the course of testing their mirrors, experienced users of the Foucault test more or less pretend, when observing the knife-edge null a narrow zone on the mirror, that they have detected this narrow zone's radius of curvature. It should now be clear to all, however, that this notion can only be a useful fiction for the mirror maker. No zone located on a paraboloid, however narrow, is really spherical, and therefore cannot have a center of curvature. But since a very narrow zone can return most of its light to a relatively precisely detectable center on the OA, we tend to think of it as in some way approximately spherical.
| Go to Another place | |
|---|---|
| Previous Page | Next Page |