On the Construction of Telescopes with Silvered Glass
Part 1

Introduction

      The differences between reflecting telescopes and achromatic refractors have long been the subject of discussion. In fact, both these instruments have rendered astonishing services to astronomy and science has adopted both of them. With reflecting telescopes of large dimensions, such as William Herschel has constructed by his own hand, one seeks a distinct and detailed perception of celestial objects. As for achromatic objectives, which can never become as large, the degree of stability which they have proven themselves capable of has made them especially good for precise observations, such as determining positions of stars and other objects. The roles thus having thus been divided, the reflecting telescope keeps its importance only if it greatly preserves its superiority with respect to its optical properties.
      In England, where the struggle has been vigorously sustained in favor of reflective instruments, large metallic mirrors remain in small numbers and the expense which they have required have not been such as to encourage numerous other experiments of the same type. Let us also add that these mirrors are so heavy that people have been reluctant to transport them up to the summits of mountains, the only points on the globe from which one has the opportunity to use the full power of such instruments.       Due to this state of things it seemed to us that it would be better to substitute glass for metal in the construction of the mirror, as long as one could coat the surface with metal after having polished it. Concerning this, the wet-process silver plating via the Drayton method leaves nothing to be desired. The cold solution, upon contact with the glass, deposits on the surface of the glass a thin layer of silver metal which, once dried, assumes a very beautiful polish when rubbed with a piece of silk impregnated with iron oxide [i.e., rouge - tr.].
      On February 16,1857 the Academy of Sciences examined a 10cm [note: is this radius or diameter? Not clear - tr.] mirror obtained as described above which, when mounted in a Newtonian telescope, produced good images and allowed a magnification of about 150 to 200 times. The mirror still has its original silver plating. It has been preserved as the first specimen to be presented to a learned society.
      [Note by Foucault in the original text: During its session of December 7, 1857, the French Academy of Sciences received a notice based on an article in the Augsbourg Gazette, concerning the opening of his workshops in Munich.) Here below we reproduce the passage in which the first attempts of M. Steinheil:
["Another interesting novelty for astronomers is the new telescope mirrors made of glass. By using Liebig's method for silvering mirror glass, metal layers can be deposited which are so good that even the rear of the silver forms a perfect mirror (or can easily be made to do so with suitable polishing agents). As a result, if normal glass is ground on only side to an exact spherical concavity, it can be silvered to give a telescope mirror which, even if it tarnishes over time, can be restored with only a little effort, as the exact shape is preserved by the glass. We have looked through a telescope of this kind with a 4" aperture which shows a marvelously clear, bright image at 100x. It is obvious that powerful telescopes can be very easily and cheaply made in this way." [(Allgemeine Zeitung, No. 84, Monday, March 24, 1856.)]
      After the presentation of the first 20 cm [this may be a typographical error; may have intended 10 cm. - tr.] diameter telescope with a 50cm focal length (interestingly a F5 mirror if the diameter was supposed to be 10cm and a F2.5 - a very short focal length - if the dimension really was 20cm - Bob), we have obtained without difficulty a second which is 22cm in diameter with a focal length of 1.5 meters (about F6.8 which is a more reasonable focal length for a telescope of that era for a fast instrument - Bob). Then, in trying to make one with a diameter of 42 cm, the workman in charge of figuring the mirror was unsuccessful at doing so, even though he tried five different times. This has forced us to recognize the limitations of the procedures ordinarily employed to produce smaller surfaces.
      Faced with the failures which threatened the hopes we had placed on this new type of mirror, we felt compelled to study the figure of the surfaces which, although worked with the greatest care, still would not produce the desired optical effect. From these studies three examining procedures have emerged which are directly applicable to concave reflecting surfaces and with the help of which one can recognize, with the required degree of precision, whether these surfaces are more or less correctly spherical. We have thus verified that opticians rarely construct surfaces which belong to the family of spheres, and that these surfaces depart all the more from spheres as they become larger. We have thus, so to speak, put our finger on an essential point which constantly recurred in the work on the 42 cm mirror, and this verification was so clear and so manifest that it suggested the idea of locally retouching the surface without altering the finish of it. This attempt, which was not at all encouraged by the expert workmen involved, nevertheless succeeded perfectly. From that moment on, our endeavors were freed from all obstacles and took on a new impetus.
      In effect, as soon as we had acquired the proof that the working of a good surface did not necessarily depend on getting everything correct at once, as soon as it was demonstrated that one could return to the job indefinitely, the development was no longer directed at arriving precisely at a sphere. Instead, we wanted to modify, by degrees, the optical surface in order to approach the parabolic curve which alone is capable of bringing all the rays from a parallel bundle to a common focus.
      The optical examination procedure which at first served to recognize the sphericity of the surfaces, modified in light of the theory of conjugate foci of an ellipse, and combined with the method of local retouching soon permitted to modify any surface of revolution furnished by the artisans from a sphere into a paraboloid, while passing through all by the intermediate ellipsoids. In this way these instruments, freed from the aberrations which compromised the clarity of their images, could be reduced to shorter focal lengths and enlarged proportionately in their three dimensions.
      We limited ourselves to telescopes with a length not more than six times the diameter of the mirror. We adopted this constant ratio between the diameter and the focal distance only after having assured ourselves that the exact convergence of the ray bundle is the only condition that must be filled in order for an instrument to give its full effect. The parabolic surface expressly fills this condition; this is why it conveys to the telescope a resolution or, as they say, an "optical power" which, if measured with care, shows itself to be independent of the focal length and to be proportional to the diameter of the mirror. In deriving precise rules for measuring these optical powers whose appreciation is somewhat arbitrary, we wanted to furnish to those who use telescopes a way of calculating directly the value optical power. Moreover, we have discovered that for any telescope of a given diameter there exists an absolute power limit. This limit depends on the physical properties of light and puts a boundary on how much magnification can be obtained.
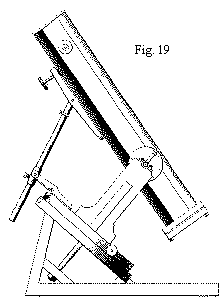
      Freed from the enormous weight of metallic mirrors and from the excessive length imposed by the use of spherical surfaces, the telescope becomes much easier to handle. We therefore added an extra benefit by placing it on a light-weight equatorial mount made of wood.
      In publishing this article, we propose not only to share the results which we have acquired, but we also want also to making known the practical procedures which have helped to obtain them. Without wishing to go into too much detail, we will put ourselves in the place of those who would like to take advantage of these same procedures and we will explain what steps to take to attain the same degree of success.
      Firstly, we will describe the various geometric optical procedures by which one explores concave spherical surfaces. Next, we will extend the general application of the same procedures to the study of surfaces having conical sections, and we will show that these examination procedures, which are called upon to keep check upon one another are more than sufficient to direct the manual work with which one intends to produce the desired surface.
      Passing thus from the application to the procedures we will borrow from the arts the means of preparing mirrors and of dealing with the surface of the glass together and of producing by local retouching a correct surface. We will discuss in detail the characteristics of a perfect surface, and we will define what we mean by optical power.
      Then we will give practical details for silvering glass surfaces, no matter how large they may be, by the Drayton procedure. We will indicate the precautions to take in order to prevent the deformation of mirrors and to adapt them to telescope tubes. We will discuss the composition of eyepieces, and we will finish with a description of a practical wooden mount particularly applicable to short focus telescopes.
Go to Another place
Previous Page Index Page Next Page