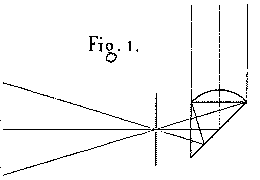
 To perform this experiment, we create a point source of light to be used as the origin of the rays to be emitted. We glue a short-focal-length plano-convex lens onto one of the two identical faces of a small, totally-reflecting right angle prism (Plate 1, figure 1). A lamp flame is placed 20 to 30 cm away from the axis of the experiment, and its horizontal rays illuminate this lens, which is perpendicular to those rays of light. The converging rays of light are completely reflected by the hypotenuse surface of the prism. These rays then form, outside of the prism, an image of the flame on a small opaque
screen. This screen is pierced by a pinhole, which we can consider to be a point. This
screen is placed near the center of curvature of the mirror and is so oriented as to fully
illuminate the mirror. A microscope is used to examine the conjugate focus.
To perform this experiment, we create a point source of light to be used as the origin of the rays to be emitted. We glue a short-focal-length plano-convex lens onto one of the two identical faces of a small, totally-reflecting right angle prism (Plate 1, figure 1). A lamp flame is placed 20 to 30 cm away from the axis of the experiment, and its horizontal rays illuminate this lens, which is perpendicular to those rays of light. The converging rays of light are completely reflected by the hypotenuse surface of the prism. These rays then form, outside of the prism, an image of the flame on a small opaque
screen. This screen is pierced by a pinhole, which we can consider to be a point. This
screen is placed near the center of curvature of the mirror and is so oriented as to fully
illuminate the mirror. A microscope is used to examine the conjugate focus.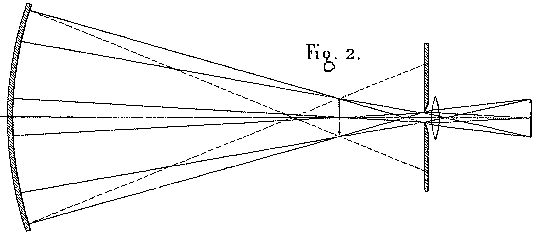 In the region around the center of curvature, we set up two straight lines, very close to each other, such as the two edges of a metal wire one millimeter in diameter. This object is illuminated by an oblique mirror, so that it is projected onto a lighted background as seen from any point on the surface of the objective mirror. The image produced is observed either with the naked eye, or, better yet, by means of a small lens, through a diaphragm with an opening of 1.5 millimeter. In this situation, the object appears as a lighted disk, whose size corresponds to the opening of the mirror. And if the edges are not straight lines, then the inflections that appear will help us to characterize the variations in the
radius of curvature. To help us understand why this is true, simply make a drawing tracing
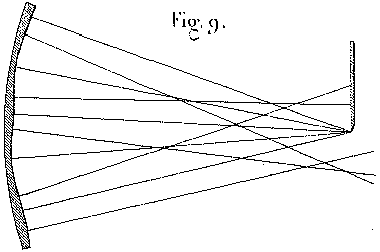
the paths of the rays of light from the surface of the mirror to the focal plane of the lens (figure 2). Then you will see how the little pinhole, by eliminating most of the rays which formed the direct image i, has the effect of composing the transmitted image i' with the rays reflected by different parts of the mirror. (This sounds a lot like a primitive version of the Ronchi Grating with only two lines in it - Bob)
In the region around the center of curvature, we set up two straight lines, very close to each other, such as the two edges of a metal wire one millimeter in diameter. This object is illuminated by an oblique mirror, so that it is projected onto a lighted background as seen from any point on the surface of the objective mirror. The image produced is observed either with the naked eye, or, better yet, by means of a small lens, through a diaphragm with an opening of 1.5 millimeter. In this situation, the object appears as a lighted disk, whose size corresponds to the opening of the mirror. And if the edges are not straight lines, then the inflections that appear will help us to characterize the variations in the
radius of curvature. To help us understand why this is true, simply make a drawing tracing
the paths of the rays of light from the surface of the mirror to the focal plane of the lens (figure 2). Then you will see how the little pinhole, by eliminating most of the rays which formed the direct image i, has the effect of composing the transmitted image i' with the rays reflected by different parts of the mirror. (This sounds a lot like a primitive version of the Ronchi Grating with only two lines in it - Bob) |
 |
 |
 |
 |
 |
 |
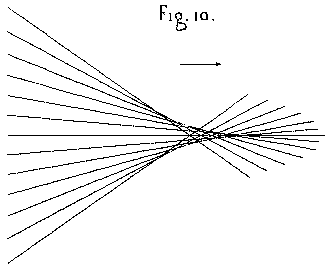 |
If we agree to consider as positive the type of aberration which results the most often from the disproportionate extension of spherical surfaces, then we will denote as negative the aberration in the opposite direction which results from an exaggerated or inopportune correction of a spherical figure. But, if we only consider the ray bundle as a whole independent of the apparatus that makes it converge, we can agree to denote as a positive aberration the arrangement of a bundle of rays wherein the central ones converge last of all. In this case the caustic (see figure 10) formed by the series of crossing rays has its vertex turned towards the side where the light is heading. By contrast, we will call a
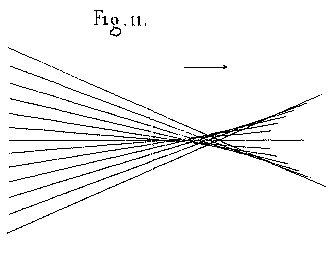
negative aberration the opposite arrangement, wherein the central parts of the ray bundle converge first, and wherein the caustic has a vertex pointing towards the mirror, as in figure 11. |
 |
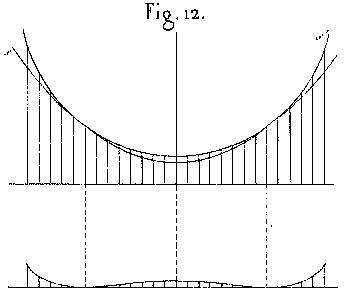
| Let us suppose, for example, that a spherical surface is examined in circumstances where it should present an ellipsoidal figure. That is to say that instead of the correct figure s (shown in figure 12) we substitute figure s' which is not correctly figured. To have an idea of the appearance which should result from this, let us put the circle and the ellipse on the same set of coordinates, and then let us construct the curve given by the changes in the differences in the y-coordinates corresponding to the same x-coordinates. This curve, which is of the fourth degree, is in fact the one which, if we imagine it rotated around the y-axis, would generate a surface that matches what we see in black-and-white shadows (figures 13 or 14) on a mirror that is examined by the third method, and when this mirror has a central zone that is a conic section, and when it has been verified as being outside the conditions defined by the positions of its own foci. |
 | |
 |
 | |
| Go to Another place | ||
|---|---|---|
| Previous Page | Index Page | Next Page |